Câu 1 trang 120 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 1 Trang 120 SGK Hình học 11 Nâng cao
Chào mừng các em học sinh đến với lời giải chi tiết Câu 1 trang 120 SGK Hình học 11 Nâng cao. Bài tập này thuộc chương trình học Hình học không gian, tập trung vào kiến thức về vectơ và ứng dụng trong giải quyết các bài toán hình học.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.
Tứ diện OABC có OA = OB = OC = a và
Đề bài
Tứ diện OABC có OA = OB = OC = a và \(\widehat {AOB} = \widehat {AOC} = 60^\circ ,\widehat {BOC} = 90^\circ \)
a. Chứng tỏ rằng ABC là tam giác vuông và OA ⊥ BC
b. Tìm đường vuông góc chung IJ của OA và BC ; tính khoảng cách giữa hai đường thẳng OA và BC.
c. Chứng minh rằng hai mặt phẳng (ABC) và (OBC) vuông góc với nhau.
Lời giải chi tiết
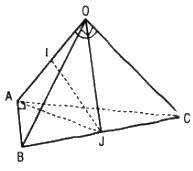
a. Vì \(\widehat {AOB} = \widehat {AOC} = 60^\circ \)
OA = OB = OC = a
Nên AB = AC = a
Suy ra ΔABC = ΔOBC
Vậy tam giác ABC vuông cân tại A
Gọi J là trung điểm của BC thì OJ ⊥ BC, AJ ⊥ BC nên OA ⊥ BC.
Cách khác:

b. Gọi I là trung điểm của OA, do OJ = AJ nên JI ⊥ OA, mà JI ⊥ BC, vậy IJ là đường vuông góc chung của OA và BC.
\(I{J^2} = O{J^2} - O{I^2} = {\left( {{{a\sqrt 2 } \over 2}} \right)^2} - {\left( {{a \over 2}} \right)^2} = {{{a^2}} \over 4}.\)
Suy ra : d(OA ; BC) = \({a \over 2}\)
c. Từ các kết quả trên ta có : OJ ⊥ BC, AJ ⊥ BC, IJ = \({1 \over 2}OA\)
Vậy góc giữa mp(OBC) và mp(ABC) bằng góc \(\widehat {OJA}\) và \(\widehat {OJA} = 90^\circ ,\) do đó mp(OBC) ⊥ mp(ABC).
Giải Chi Tiết Câu 1 Trang 120 SGK Hình Học 11 Nâng Cao
Câu 1 trang 120 SGK Hình học 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về vectơ để chứng minh một đẳng thức vectơ. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các quy tắc cộng, trừ, nhân vectơ với một số thực và các tính chất của vectơ.
Nội Dung Bài Toán
Bài toán thường có dạng: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng: vectơ AM = (1/2)vectơ AB + (1/2)vectơ AC
Phương Pháp Giải
Để chứng minh đẳng thức vectơ, chúng ta có thể sử dụng một trong các phương pháp sau:
- Phân tích vectơ: Biểu diễn vectơ cần chứng minh thông qua các vectơ đã cho.
- Sử dụng quy tắc hình bình hành: Nếu vectơ cần chứng minh là tổng của hai vectơ, ta có thể sử dụng quy tắc hình bình hành để kiểm tra.
- Sử dụng tọa độ vectơ: Chọn hệ tọa độ thích hợp và biểu diễn các vectơ bằng tọa độ. Sau đó, kiểm tra xem đẳng thức vectơ có đúng hay không.
Lời Giải Chi Tiết
Trong trường hợp bài toán trên, chúng ta sẽ sử dụng phương pháp phân tích vectơ.
Ta có: vectơ AM = vectơ AB + vectơ BM
Vì M là trung điểm của BC, nên vectơ BM = (1/2)vectơ BC
Mà vectơ BC = vectơ AC - vectơ AB
Do đó, vectơ BM = (1/2)(vectơ AC - vectơ AB)
Thay vào biểu thức của vectơ AM, ta được:
vectơ AM = vectơ AB + (1/2)(vectơ AC - vectơ AB) = vectơ AB + (1/2)vectơ AC - (1/2)vectơ AB = (1/2)vectơ AB + (1/2)vectơ AC
Vậy, ta đã chứng minh được vectơ AM = (1/2)vectơ AB + (1/2)vectơ AC
Lưu Ý Quan Trọng
- Nắm vững các quy tắc cộng, trừ, nhân vectơ với một số thực.
- Hiểu rõ các tính chất của vectơ, như tính giao hoán, tính kết hợp, tính chất phân phối.
- Luyện tập thường xuyên để làm quen với các dạng bài tập về vectơ.
Bài Tập Tương Tự
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
- Bài 2 trang 120 SGK Hình học 11 Nâng cao
- Bài 3 trang 120 SGK Hình học 11 Nâng cao
Kết Luận
Việc giải Câu 1 trang 120 SGK Hình học 11 Nâng cao đòi hỏi chúng ta phải có kiến thức vững chắc về vectơ và khả năng vận dụng linh hoạt các quy tắc và tính chất của vectơ. Hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về bài toán và tự tin giải quyết các bài tập tương tự.
Mọi thắc mắc hoặc cần hỗ trợ thêm, đừng ngần ngại liên hệ với tusach.vn. Chúng tôi luôn sẵn sàng đồng hành cùng các em trên con đường chinh phục tri thức!