Câu 39 trang 68 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Bài Tập Hình Học 11 Nâng Cao - Câu 39 Trang 68
Câu 39 trang 68 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian để giải quyết các vấn đề thực tế.
Tại tusach.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và chính xác nhất cho câu hỏi này, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
Cho hình chóp cụt ABC.A’B’C’ có đáy lớn ABC và các cạnh bên AA’, BB’, CC’. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và M’, N’, P’ lần lượt là trung điểm của các cạnh A’B’, B’C’, C’A’. Chứng minh MNP.M’N’P’ là hình chóp cụt
Đề bài
Cho hình chóp cụt ABC.A’B’C’ có đáy lớn ABC và các cạnh bên AA’, BB’, CC’. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và M’, N’, P’ lần lượt là trung điểm của các cạnh A’B’, B’C’, C’A’. Chứng minh MNP.M’N’P’ là hình chóp cụt
Lời giải chi tiết
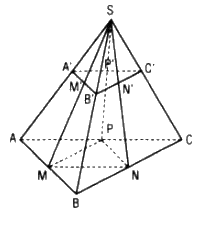
Gọi S là giao điểm các cạnh bên AA’, BB’, CC’của hình chóp cụt.
Do A’B’ // AB và M’, M lần lượt là trung điểm của A’B’, AB nên MM’ đi qua S.
Tương tự NN’, PP’ cùng đi qua S.
Vậy MM’, NN’, PP’ đồng quy tại S.
Ta có (M’N’P’) // (MNP) nên MNP.M’N’P’ là hình chóp cụt.
Giải Chi Tiết Câu 39 Trang 68 SGK Hình Học 11 Nâng Cao
Câu 39 trang 68 SGK Hình học 11 Nâng cao thường liên quan đến việc xác định mối quan hệ giữa các vectơ, kiểm tra tính đồng phẳng của ba vectơ, hoặc tìm điều kiện để ba điểm thẳng hàng. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về:
- Vectơ: Định nghĩa, các phép toán trên vectơ (cộng, trừ, nhân với một số), tích vô hướng, tích có hướng.
- Đường thẳng trong không gian: Phương trình tham số, phương trình chính tắc, vị trí tương đối giữa hai đường thẳng.
- Mặt phẳng trong không gian: Phương trình mặt phẳng, vị trí tương đối giữa đường thẳng và mặt phẳng, giữa hai mặt phẳng.
Phân Tích Bài Toán và Lập Kế Hoạch Giải
Trước khi bắt tay vào giải, hãy đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lập kế hoạch giải bằng cách:
- Chọn hệ tọa độ thích hợp: Việc chọn hệ tọa độ phù hợp sẽ giúp đơn giản hóa bài toán và dễ dàng tính toán.
- Biểu diễn các vectơ, điểm, đường thẳng, mặt phẳng bằng phương trình: Sử dụng các công thức và kiến thức đã học để biểu diễn các yếu tố của bài toán bằng phương trình.
- Vận dụng các công cụ toán học: Sử dụng các công cụ như tích vô hướng, tích có hướng, định thức để giải quyết bài toán.
Lời Giải Chi Tiết Câu 39 Trang 68 (Ví dụ minh họa - đề bài có thể thay đổi)
Giả sử đề bài: Cho bốn điểm A(1; 2; 3), B(2; 3; 4), C(3; 4; 5), D(4; 5; 6). Chứng minh rằng bốn điểm A, B, C, D đồng phẳng.
Lời giải:
Để chứng minh bốn điểm A, B, C, D đồng phẳng, ta cần chứng minh rằng bốn vectơ AB, AC, AD đồng phẳng. Điều này tương đương với việc chứng minh tích hỗn hợp của ba vectơ này bằng 0.
Ta có:
- AB = (2-1; 3-2; 4-3) = (1; 1; 1)
- AC = (3-1; 4-2; 5-3) = (2; 2; 2)
- AD = (4-1; 5-2; 6-3) = (3; 3; 3)
Tích hỗn hợp của AB, AC, AD là:
[AB, AC, AD] = AB . (AC x AD)
Tính tích có hướng AC x AD:
AC x AD = (2*3 - 2*3; 2*3 - 2*3; 2*3 - 2*3) = (0; 0; 0)
Do đó, [AB, AC, AD] = AB . (0; 0; 0) = 0
Vậy, bốn điểm A, B, C, D đồng phẳng.
Lưu Ý Khi Giải Bài Tập
Khi giải các bài tập về vectơ, đường thẳng và mặt phẳng trong không gian, cần chú ý:
- Kiểm tra kỹ các điều kiện của bài toán.
- Sử dụng đúng các công thức và định lý.
- Biết cách chọn hệ tọa độ phù hợp.
- Kiểm tra lại kết quả sau khi giải xong.
Hy vọng với lời giải chi tiết và những lưu ý trên, bạn sẽ tự tin hơn khi giải Câu 39 trang 68 SGK Hình học 11 Nâng cao và các bài tập tương tự. Chúc bạn học tốt!