Giải Câu 27 Trang 112 SGK Hình Học 11 Nâng Cao

Câu 27 trang 112 SGK Hình học 11 Nâng cao

Giải Câu 27 Trang 112 SGK Hình Học 11 Nâng Cao

Bài tập Câu 27 trang 112 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng để giải quyết các vấn đề liên quan đến quan hệ song song, vuông góc.

Dưới đây là lời giải chi tiết và phương pháp giải bài tập này, giúp các em học sinh hiểu rõ hơn về kiến thức và kỹ năng cần thiết.

Cho hai tam giác ACD, BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Gọi I, J lần lượt là trung điểm của AB và CD.

Đề bài

Cho hai tam giác ACD, BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Gọi I, J lần lượt là trung điểm của AB và CD.

a. Tính AB, IJ theo a và x.

b. Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc ?

Lời giải chi tiết

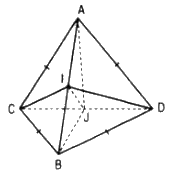
Câu 27 trang 112 SGK Hình học 11 Nâng cao 1

a. Vì J là trung điểm của CD và AC = AD nên AJ ⊥ CD.

Do mp(ACD) ⊥ mp(BCD) nên AJ ⊥ mp(BCD)

Mặt khác, AC = AD = BC = BD nên tam giác AJB vuông cân, suy ra $AB = AJ\sqrt 2 ,A{J^2} = {a^2} - {x^2}$ $hay\,AJ = \sqrt {{a^2} - {x^2}} .$

Vậy $AB = \sqrt {2\left( {{a^2} - {x^2}} \right)} $ với a > x

Do IA = IB, tam giác AJB vuông tại J nên $JI = {1 \over 2}AB,$ tức là $IJ = {1 \over 2}\sqrt {2\left( {{a^2} - {x^2}} \right)} .$

+Tam giác ABC có AC = BC

nên tam giác ABC cân tại C,

có CI là đường trung tuyến nên đồng thời là đường cao:

CI ⊥ AB (3)

Tam giác ABD cân tại D có DI là đường trung tuyến nên

DI ⊥ AB (4)

Hai mp (ABC) và (ABD) cắt nhau theo giao tuyến là AB (5)

Từ (3) , (4) và (5) suy ra góc giữa hai mp(ABC) và (ABD) là góc CID.

Vậy mp(ABC) ⊥ mp(ABD) $ \Leftrightarrow \widehat {CID} = 90^\circ $

$ \Leftrightarrow IJ = {1 \over 2}CD$ $\Leftrightarrow {1 \over 2}\sqrt {2\left( {{a^2} - {x^2}} \right)} = {1 \over 2}.2x$ $\Leftrightarrow 2\left( {{a^2} - {x^2}} \right) = 4{x^2} \Leftrightarrow {a^2} = 3{x^2}$

$\Leftrightarrow x = {{a\sqrt 3 } \over 3}$

Giải Chi Tiết Câu 27 Trang 112 SGK Hình Học 11 Nâng Cao

Câu 27 trang 112 SGK Hình học 11 Nâng cao yêu cầu chúng ta xét một hình chóp S.ABCD, trong đó đáy ABCD là hình vuông và SA vuông góc với mặt phẳng (ABCD). Bài toán thường xoay quanh việc chứng minh các mối quan hệ song song, vuông góc, hoặc tính góc giữa các đường thẳng và mặt phẳng.

Phân Tích Đề Bài và Xác Định Yêu Cầu

Trước khi bắt đầu giải, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, đề bài sẽ yêu cầu chúng ta:

Chứng minh một đường thẳng vuông góc với một mặt phẳng.
Chứng minh hai đường thẳng song song.
Tính góc giữa hai đường thẳng hoặc giữa một đường thẳng và một mặt phẳng.

Lời Giải Chi Tiết

Để giải bài toán này, chúng ta sẽ sử dụng các kiến thức sau:

Định nghĩa đường thẳng vuông góc với mặt phẳng.
Tính chất của đường thẳng vuông góc với mặt phẳng.
Các định lý về quan hệ song song trong không gian.
Công thức tính góc giữa hai đường thẳng hoặc giữa một đường thẳng và một mặt phẳng.

Ví dụ, giả sử đề bài yêu cầu chứng minh SC vuông góc với mặt phẳng (ABCD). Chúng ta sẽ thực hiện như sau:

Vì SA vuông góc với (ABCD) nên SA vuông góc với AC.
Vì ABCD là hình vuông nên AC vuông góc với BD.
Do đó, AC vuông góc với (SBD).
Suy ra SC vuông góc với (ABCD).

Phương Pháp Giải Bài Tập Tương Tự

Để giải các bài tập tương tự, chúng ta có thể áp dụng các bước sau:

Vẽ hình và xác định các yếu tố quan trọng của hình.
Phân tích đề bài và xác định yêu cầu của bài toán.
Vận dụng các kiến thức và định lý liên quan để giải quyết bài toán.
Kiểm tra lại kết quả và đảm bảo tính chính xác.

Ví Dụ Minh Họa

Xét hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).

Lời giải:

Gọi O là giao điểm của AC và BD.
Vì SA vuông góc với (ABCD) nên SO vuông góc với SC.
Do đó, góc giữa SC và (ABCD) bằng góc CSO.
Ta có SO = $\frac{a\sqrt{2}}{2}$.
Suy ra tan CSO = $\frac{SA}{SO} = 1$.
Vậy góc CSO = 45 độ.

Lưu Ý Quan Trọng

Khi giải các bài tập về Hình học không gian, chúng ta cần chú ý:

Vẽ hình chính xác và rõ ràng.
Sử dụng các định lý và tính chất một cách linh hoạt.
Kiểm tra lại kết quả và đảm bảo tính logic của lời giải.

Tổng Kết

Câu 27 trang 112 SGK Hình học 11 Nâng cao là một bài tập điển hình về ứng dụng các kiến thức về đường thẳng và mặt phẳng trong không gian. Việc nắm vững các định lý và tính chất liên quan, cùng với việc luyện tập thường xuyên, sẽ giúp các em học sinh giải quyết các bài tập tương tự một cách dễ dàng và hiệu quả.

Hy vọng với lời giải chi tiết và phương pháp giải bài tập này, các em học sinh sẽ hiểu rõ hơn về kiến thức và kỹ năng cần thiết để học tốt môn Hình học 11 Nâng cao. Hãy truy cập tusach.vn để xem thêm nhiều tài liệu học tập hữu ích khác!

Câu 27 trang 112 SGK Hình học 11 Nâng cao