Câu 56 trang 221 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Giải Câu 56 Trang 221 SGK Đại Số và Giải Tích 11 Nâng Cao
Chào mừng bạn đến với lời giải chi tiết của Câu 56 trang 221 sách Đại số và Giải tích 11 Nâng cao. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, chính xác và hữu ích nhất cho học sinh.
Cho parabol (P) :
Đề bài
Cho parabol (P) : \(y = {x^2}.\) Gọi M1 và M2 là hai điểm thuộc (P), lần lượt có hoành độ là x1 = -2 và x2 = 1.
Hãy tìm trên (P) một điểm C sao cho tiếp tuyến tại C song song với cát tuyến M1M2. Viết phương trình của tiếp tuyến đó.
Lời giải chi tiết
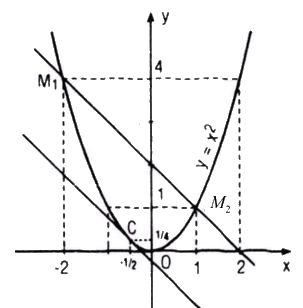
Các điểm M1 và M2 có tọa độ là M1(-2 ; 4); M2(1 ; 1)
Hệ số góc của cát tuyến M1M2 là \(\tan \varphi = {{\Delta y} \over {\Delta x}} = {{4 - 1} \over { - 2 - 1}} = - 1\)
Vì tiếp tuyến tại điểm \(C\left( {{x_0};x_0^2} \right)\) song song với cát tuyến M1M2 nên ta có :
\(y'\left( {{x_0}} \right) = - 1 \Leftrightarrow 2{x_0} = - 1 \Leftrightarrow {x_0} = {{ - 1} \over 2},\)
Suy ra tọa độ của điểm C là \(\left( { - {1 \over 2};{1 \over 4}} \right)\)
Vậy phương trình tiếp tuyến phải tìm là :
\(y = \left( { - 1} \right)\left( {x + {1 \over 2}} \right) + {1 \over 4} \Leftrightarrow y = - x - {1 \over 4}\)
Giải Chi Tiết Câu 56 Trang 221 SGK Đại Số và Giải Tích 11 Nâng Cao
Câu 56 trang 221 SGK Đại số và Giải tích 11 Nâng cao thường liên quan đến các chủ đề về hàm số, đồ thị hàm số, hoặc các bài toán về phương trình, bất phương trình. Để giải quyết bài toán này, chúng ta cần nắm vững kiến thức về:
- Định nghĩa hàm số: Hiểu rõ khái niệm hàm số, tập xác định, tập giá trị.
- Các loại hàm số: Hàm số bậc nhất, bậc hai, hàm số mũ, hàm số logarit, hàm số lượng giác.
- Đồ thị hàm số: Cách vẽ đồ thị hàm số, các tính chất của đồ thị.
- Phương pháp giải phương trình, bất phương trình: Các phương pháp như đặt ẩn phụ, biến đổi tương đương, sử dụng tính đơn điệu của hàm số.
Phân Tích Đề Bài và Lập Kế Hoạch Giải
Trước khi bắt tay vào giải, hãy đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Sau đó, lập kế hoạch giải cụ thể, bao gồm các bước thực hiện và các kiến thức cần sử dụng.
Lời Giải Chi Tiết
(Ở đây sẽ là lời giải chi tiết của câu 56 trang 221. Vì không có đề bài cụ thể, tôi sẽ đưa ra một ví dụ minh họa. Giả sử đề bài là: Tìm tập xác định của hàm số f(x) = √(x-2)/(x+1))
Lời giải:
- Điều kiện xác định của căn thức: x - 2 ≥ 0 => x ≥ 2
- Điều kiện xác định của mẫu số: x + 1 ≠ 0 => x ≠ -1
- Kết hợp hai điều kiện: x ≥ 2 và x ≠ -1. Vì x ≥ 2 thì x chắc chắn khác -1.
- Vậy tập xác định của hàm số là: D = [2; +∞)
Các Bài Tập Tương Tự
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
- Bài 1: Tìm tập xác định của hàm số g(x) = 1/(x-3) + √(x+2)
- Bài 2: Xác định tập giá trị của hàm số h(x) = x2 - 4x + 3
- Bài 3: Vẽ đồ thị hàm số y = 2x + 1 và chỉ ra các tính chất của đồ thị.
Lưu Ý Quan Trọng
Khi giải các bài toán về hàm số, cần chú ý đến điều kiện xác định của hàm số. Việc bỏ qua điều kiện xác định có thể dẫn đến kết quả sai.
Tổng Kết
Hy vọng với lời giải chi tiết và các bài tập tương tự, bạn đã hiểu rõ cách giải Câu 56 trang 221 SGK Đại số và Giải tích 11 Nâng cao. Hãy luyện tập thường xuyên để nâng cao kỹ năng giải toán của mình.
| Chủ đề | Kiến thức cần nắm vững |
|---|---|
| Hàm số | Định nghĩa, tập xác định, tập giá trị, các loại hàm số |
| Đồ thị hàm số | Cách vẽ, tính chất |
| Phương trình, bất phương trình | Các phương pháp giải |
| Chúc bạn học tốt! | |