Câu 18 trang 226 SGK Đại số và Giải tích 11 Nâng cao
Bài tập Câu 18 trang 226 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.
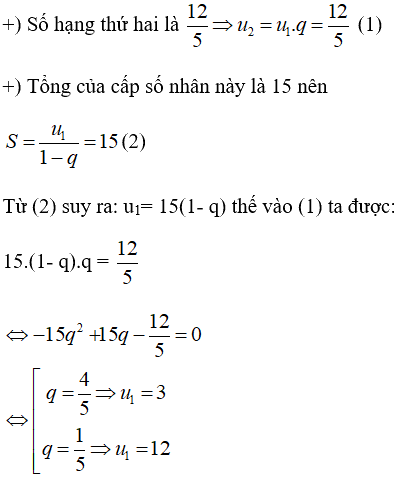
Giải Chi Tiết Câu 18 Trang 226 SGK Đại số và Giải tích 11 Nâng cao
Câu 18 trang 226 SGK Đại số và Giải tích 11 Nâng cao thường liên quan đến việc tìm đạo hàm của hàm số, xét tính đơn điệu của hàm số, hoặc tìm cực trị của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
- Định nghĩa đạo hàm: Đạo hàm của hàm số f(x) tại điểm x0 là giới hạn của tỷ số \frac{f(x) - f(x_0)}{x - x_0}\ khi x tiến tới x0.
- Các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Đạo hàm của các hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
Lời Giải Chi Tiết
Để minh họa, giả sử đề bài Câu 18 như sau:
Cho hàm số y = x3 - 3x2 + 2. Tìm khoảng đồng biến, nghịch biến của hàm số.
- Tính đạo hàm: y' = 3x2 - 6x
- Tìm điểm dừng: Giải phương trình y' = 0, ta được x = 0 và x = 2.
- Xét dấu đạo hàm:
- Khi x < 0: y' > 0, hàm số đồng biến.
- Khi 0 < x < 2: y' < 0, hàm số nghịch biến.
- Khi x > 2: y' > 0, hàm số đồng biến.
- Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Các Dạng Bài Tập Tương Tự
Ngoài bài tập Câu 18 trang 226, học sinh có thể gặp các dạng bài tập tương tự như:
- Tìm đạo hàm cấp hai.
- Khảo sát hàm số bằng đạo hàm (tìm cực trị, điểm uốn, khoảng lồi, khoảng lõm).
- Ứng dụng đạo hàm để giải các bài toán tối ưu.
Mẹo Giải Bài Tập Đạo Hàm
Để giải các bài tập về đạo hàm một cách hiệu quả, học sinh nên:
- Nắm vững các định nghĩa và quy tắc tính đạo hàm.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán.
- Kiểm tra lại kết quả sau khi giải xong.
Tài Liệu Tham Khảo
Học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Đại số và Giải tích:
- Sách giáo khoa Đại số và Giải tích 11 Nâng cao.
- Sách bài tập Đại số và Giải tích 11 Nâng cao.
- Các trang web học toán trực tuyến như tusach.vn, VietJack, Hoc24.
Kết Luận
Câu 18 trang 226 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và các gợi ý trên, các em học sinh sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tốt!
