Câu 17 trang 226 SGK Đại số và Giải tích 11 Nâng cao
Tổng quan nội dung
Câu 17 trang 226 SGK Đại số và Giải tích 11 Nâng cao
Bài tập này thuộc chương trình Đại số và Giải tích 11 Nâng cao, tập trung vào việc vận dụng kiến thức về hàm số, đạo hàm để giải quyết các bài toán thực tế.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững phương pháp và tự tin giải các bài tập tương tự.
Tính các giới hạn sau :
LG a
\(\lim \sqrt {3{n^4} - 10n + 12} \)
Lời giải chi tiết:
\(\lim \sqrt {3{n^4} - 10n + 12} \) \(= \lim {n^2}.\sqrt {3 - {{10} \over {{n^3}}} + {{12} \over {{n^4}}}} \) \(= + \infty \)
Vì
\(\left\{ \begin{array}{l}\lim {n^2} = + \infty \\\lim \sqrt {3 - \frac{{10}}{{{n^3}}} + \frac{{12}}{{{n^4}}}} = \sqrt 3 > 0\end{array} \right.\)
LG b
\(\lim \left( {{{2.3}^n} - {{5.4}^n}} \right)\)
Lời giải chi tiết:
\(\lim \left( {{{2.3}^n} - {{5.4}^n}} \right) \) \(= \lim {4^n}\left[ {2{{\left( {{3 \over 4}} \right)}^n} - 5} \right] = - \infty \)
Vì
\(\left\{ \begin{array}{l}\lim {4^n} = + \infty \\\lim \left( {2.{{\left( {\frac{3}{4}} \right)}^n} - 5} \right) = - 5 < 0\end{array} \right.\)
LG c
\(\lim \left( {\sqrt {{n^4} + {n^2} + 1} - {n^2}} \right)\)
Lời giải chi tiết:
\(\eqalign{ & \lim \left( {\sqrt {{n^4} + {n^2} + 1} - {n^2}} \right) \cr& = \lim \frac{{\left( {\sqrt {{n^4} + {n^2} + 1} - {n^2}} \right)\left( {\sqrt {{n^4} + {n^2} + 1} + {n^2}} \right)}}{{\sqrt {{n^4} + {n^2} + 1} + {n^2}}} \cr &= \lim \frac{{{n^4} + {n^2} + 1 - {n^4}}}{{\sqrt {{n^4} + {n^2} + 1} + {n^2}}}\cr &= \lim {{{n^2} + 1} \over {\sqrt {{n^4} + {n^2} + 1} + {n^2}}} \cr & = \lim \frac{{{n^2} + 1}}{{\sqrt {{n^4}\left( {1 + \frac{1}{{{n^2}}} + \frac{1}{{{n^4}}}} \right)} + {n^2}}} \cr & = \lim \frac{{{n^2}\left( {1 + \frac{1}{{{n^2}}}} \right)}}{{{n^2}\sqrt {1 + \frac{1}{{{n^2}}} + \frac{1}{{{n^4}}}} + {n^2}}} \cr & = \lim \frac{{{n^2}\left( {1 + \frac{1}{{{n^2}}}} \right)}}{{{n^2}\left( {\sqrt {1 + \frac{1}{{{n^2}}} + \frac{1}{{{n^4}}}} + 1} \right)}}\cr & = \lim {{1 + {1 \over {{n^2}}}} \over {\sqrt {1 + {1 \over {{n^2}}} + {1 \over {{n^4}}}} + 1}} \cr & = \frac{{1 + 0}}{{\sqrt {1 + 0 + 0} + 1}}= {1 \over 2} \cr} \)
LG d
\(\lim {1 \over {\sqrt {{n^2} + 2n} - n}}\)
Lời giải chi tiết:
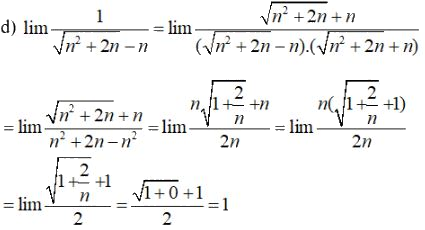
Giải chi tiết Câu 17 trang 226 SGK Đại số và Giải tích 11 Nâng cao
Câu 17 trang 226 SGK Đại số và Giải tích 11 Nâng cao yêu cầu chúng ta vận dụng kiến thức về đạo hàm của hàm số để tìm cực trị và khảo sát hàm số. Dưới đây là lời giải chi tiết:
Đề bài:
Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy tìm các điểm cực trị của hàm số.
Lời giải:
- Tính đạo hàm bậc nhất:
- Tìm các điểm làm đạo hàm bậc nhất bằng 0:
- Khảo sát dấu của đạo hàm bậc nhất:
- Kết luận:
f'(x) = 3x2 - 6x
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Các bài tập tương tự:
- Bài 1: Tìm cực trị của hàm số y = x3 - 6x2 + 9x - 2
- Bài 2: Khảo sát hàm số y = 2x3 - 3x2 + 1
- Bài 3: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = -x3 + 3x2 - 2 trên đoạn [-1; 3]
Mẹo giải nhanh:
Để giải nhanh các bài tập về cực trị, bạn nên nhớ các bước sau:
- Tính đạo hàm bậc nhất f'(x).
- Giải phương trình f'(x) = 0 để tìm các điểm nghi ngờ là cực trị.
- Khảo sát dấu của đạo hàm bậc nhất để xác định loại cực trị (cực đại hoặc cực tiểu).
- Tính giá trị của hàm số tại các điểm cực trị.
Lưu ý quan trọng:
Khi khảo sát hàm số, bạn cần chú ý đến tập xác định của hàm số và các điểm không xác định của đạo hàm. Ngoài ra, bạn cũng nên vẽ đồ thị của hàm số để kiểm tra lại kết quả.
Hy vọng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải Câu 17 trang 226 SGK Đại số và Giải tích 11 Nâng cao. Chúc các em học tốt!