Giải Câu 31 Trang 117 SGK Hình Học 11 Nâng Cao

Câu 31 trang 117 SGK Hình học 11 Nâng cao

Giải Câu 31 Trang 117 SGK Hình Học 11 Nâng Cao

Chào các em học sinh! Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho Câu 31 trang 117 sách giáo khoa Hình học 11 Nâng cao. Chúng tôi sẽ giúp các em nắm vững kiến thức và phương pháp giải bài tập một cách hiệu quả.

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BC’ và CD’

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BC’ và CD’

Lời giải chi tiết

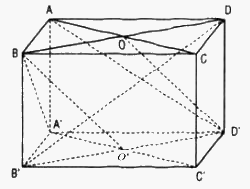
Gọi O, O’ lần lượt là tâm các hình vuông ABCD, A’B’C’D’ của hình lập phương ABCD.A’B’C’D’ cạnh a.

* Ta chứng minh B’D ⊥ (BA’C) và B’D ⊥ (ACD’)

Ta có: \(\left\{ {\matrix{ {A'C' \bot B'D'} \cr {A'C' \bot BB'} \cr } } \right. \Rightarrow A'C' \bot \left( {BB'D'D} \right)\)

Mà B’D ⊂ (BB’D’D) nên B’D ⊥ A’C’ (1)

Tương tự \(\left\{ {\matrix{ {AB' \bot A'B} \cr {A'B \bot B'C'} \cr } } \right. \Rightarrow A'B \bot \left( {AB'C'D} \right)\)

Mà B’D ⊂ (AB’C’D) nên B’D ⊥ A’B (2)

Từ (1) và (2) suy ra B’D ⊥ (BA’C’)

Tương tự ta cũng chứng minh được B’D ⊥ (ACD’)

* Hai mặt phẳng (BA’C’) và (ACD’) song song với nhau, vuông góc với đoạn B’D và chia B’D thành 3 phần bằng nhau (xét hình bình hành BB’DD’ và BO // D’O')

Do đó khoảng cách giữa mp(BA’C) và mp(ACD’) là \({{B'D} \over 3} = {{a\sqrt 3 } \over 3}\)

* Khoảng cách giữa BC’ và CD’

Khoảng cách giữa hai đường thẳng chéo nhau BC’ và CD’ bằng khoảng cách giữa hai mặt phẳng song song : mp(BA’C’) và mp(ACD’).

Vậy khoảng cách đó là \({{a\sqrt 3 } \over 3}\)

Giải Chi Tiết Câu 31 Trang 117 SGK Hình Học 11 Nâng Cao

Câu 31 trang 117 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học, thường liên quan đến các kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các định nghĩa, tính chất và định lý liên quan.

Nội Dung Bài Toán

Thông thường, câu 31 trang 117 sẽ yêu cầu học sinh thực hiện một trong các nhiệm vụ sau:

Xác định mối quan hệ giữa các vectơ.
Chứng minh ba điểm thẳng hàng hoặc ba điểm không thẳng hàng.
Tìm giao điểm của đường thẳng và mặt phẳng.
Xác định góc giữa hai đường thẳng hoặc giữa đường thẳng và mặt phẳng.
Tính khoảng cách từ một điểm đến mặt phẳng.

Phương Pháp Giải

Để giải quyết bài toán này một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:

Sử dụng các định nghĩa và tính chất cơ bản: Nắm vững các định nghĩa về vectơ, đường thẳng, mặt phẳng và các tính chất liên quan.
Áp dụng các định lý: Sử dụng các định lý về mối quan hệ giữa các vectơ, điều kiện đồng phẳng của ba vectơ, điều kiện song song hoặc vuông góc của hai đường thẳng hoặc hai mặt phẳng.
Sử dụng phương pháp tọa độ: Chuyển bài toán vào hệ tọa độ để giải quyết bằng các công cụ đại số.
Vẽ hình: Vẽ hình minh họa để trực quan hóa bài toán và tìm ra hướng giải quyết.

Lời Giải Chi Tiết

(Ở đây sẽ là lời giải chi tiết cho câu 31 trang 117, tùy thuộc vào nội dung cụ thể của bài toán. Ví dụ:)

Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M là trung điểm của CD. Biết SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SM và mặt phẳng (ABCD).

Lời giải:

Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABCD). Vì SA vuông góc với (ABCD) nên H trùng với A.
Xét tam giác SAM vuông tại A, ta có: tan(góc giữa SM và (ABCD)) = tan(góc SMA) = SA/AM = a/(a/2) = 2.
Vậy, góc giữa đường thẳng SM và mặt phẳng (ABCD) là arctan(2).

Lưu Ý Quan Trọng

Khi giải các bài toán về hình học không gian, học sinh cần chú ý:

Đọc kỹ đề bài và xác định đúng yêu cầu của bài toán.
Vẽ hình minh họa chính xác và rõ ràng.
Sử dụng các công cụ đại số và hình học một cách linh hoạt.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Bài Tập Tương Tự

Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo các bài tập tương tự sau:

Bài 32 trang 117 SGK Hình học 11 Nâng cao.
Bài 33 trang 117 SGK Hình học 11 Nâng cao.
Các bài tập trong sách bài tập Hình học 11 Nâng cao.

Kết Luận

Hy vọng bài viết này đã cung cấp cho các em những kiến thức và phương pháp giải bài tập hiệu quả cho Câu 31 trang 117 SGK Hình học 11 Nâng cao. Chúc các em học tập tốt!

Câu 31 trang 117 SGK Hình học 11 Nâng cao