Giải Câu 12 Trang 17 SGK Đại Số và Giải Tích 11 Nâng Cao

Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao

Giải Câu 12 Trang 17 SGK Đại Số và Giải Tích 11 Nâng Cao

Bài tập Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.

a. Từ đồ thị của hàm số y = cosx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó :

LG a

Từ đồ thị của hàm số \(y = \cos x\), hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó:

\(y = \cos x + 2\)

\(y = \cos \left( {x - {\pi \over 4}} \right)\)

Phương pháp giải:

Sử dụng lý thuyết tịnh tiến đồ thị:

Cho hàm số y=f(x) có đồ thị (C). Khi đó,

+) Hàm số y=f(x)+p có được do tịnh tiến (C) lên trên p đơn vị (p > 0)

+) Hàm số y=f(x-q) có được do tịnh tiến (C) sang phải q đơn vị (q > 0)

Lời giải chi tiết:

Đồ thị của hàm số \(y = \cos x + 2\) có được do tịnh tiến đồ thị của hàm số \(y = \cos x\) lên trên một đoạn có độ dài bằng \(2\)

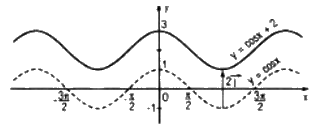
Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao 1

Đồ thị của hàm số \(y = \cos \left( {x - {\pi \over 4}} \right)\) có được do tịnh tiến đồ thị của hàm số y = cosx sang phải một đoạn có độ dài \({\pi \over 4}\)

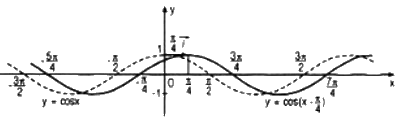
Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao 2

LG b

Hỏi mỗi hàm số đó có phải là hàm số tuần hoàn không ?

Lời giải chi tiết:

Các hàm số trên đều là hàm tuần hoàn vì:

nếu \(f(x) = \cos x + 2\) thì \(f(x + 2π) = \cos(x + 2π) + 2\)

\(= \cos x + 2 = f(x), ∀x \in\mathbb R\)

Và nếu \(g(x) = \cos \left( {x - {\pi \over 4}} \right)\) thì:

\(g(x + 2π) = \cos \left( {x + 2\pi - {\pi \over 4}} \right)\)

\(=\cos \left( {x - {\pi \over 4}} \right) = g\left( x \right)\) , \(∀x \in\mathbb R\)

Giải Chi Tiết Câu 12 Trang 17 SGK Đại Số và Giải Tích 11 Nâng Cao

Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao thường xoay quanh việc xét tính đơn điệu của hàm số, tìm khoảng đồng biến, nghịch biến, hoặc xác định các điểm cực trị. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản sau:

Định nghĩa hàm số đơn điệu: Hàm số f(x) được gọi là đồng biến trên khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) ≤ f(x2). Hàm số f(x) được gọi là nghịch biến trên khoảng (a, b) nếu với mọi x1, x2 thuộc (a, b) và x1 < x2 thì f(x1) ≥ f(x2).
Đạo hàm và tính đơn điệu: Nếu f'(x) > 0 trên khoảng (a, b) thì hàm số f(x) đồng biến trên (a, b). Nếu f'(x) < 0 trên khoảng (a, b) thì hàm số f(x) nghịch biến trên (a, b).
Điểm cực trị: Điểm x0 được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng mở (a, b) chứa x0 sao cho f(x) ≤ f(x0) với mọi x thuộc (a, b). Điểm x0 được gọi là điểm cực tiểu của hàm số f(x) nếu tồn tại một khoảng mở (a, b) chứa x0 sao cho f(x) ≥ f(x0) với mọi x thuộc (a, b).

Ví dụ minh họa (giả định nội dung câu 12):

Đề bài: Xét hàm số f(x) = x³ - 3x² + 2. Tìm khoảng đồng biến, nghịch biến và các điểm cực trị của hàm số.

Giải:

Tính đạo hàm: f'(x) = 3x² - 6x
Tìm điểm dừng: Giải phương trình f'(x) = 0, ta được x = 0 hoặc x = 2.
Xét dấu đạo hàm:
x -∞ 0 2 +∞
f'(x) + - +
f(x) Đồng biến Nghịch biến Đồng biến
Kết luận:
- Hàm số đồng biến trên các khoảng (-∞, 0) và (2, +∞).
- Hàm số nghịch biến trên khoảng (0, 2).
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.

x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	Đồng biến	Nghịch biến	Đồng biến

Lưu ý: Đây chỉ là một ví dụ minh họa. Nội dung cụ thể của Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao có thể khác. Học sinh cần đọc kỹ đề bài và áp dụng các kiến thức đã học để giải quyết bài toán.

Tusach.vn – Nguồn tài liệu học tập uy tín

Tusach.vn cung cấp đầy đủ các tài liệu học tập, đáp án, lời giải bài tập cho các môn học từ lớp 6 đến lớp 12. Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho học sinh những kiến thức chính xác, dễ hiểu và hiệu quả. Hãy truy cập tusach.vn để học tập tốt hơn!

Ngoài ra, bạn có thể tìm thấy các tài liệu liên quan như:

Giải bài tập Đại số và Giải tích 11 nâng cao
Lý thuyết Đại số và Giải tích 11 nâng cao
Đề thi thử Đại số và Giải tích 11 nâng cao

Câu 12 trang 17 SGK Đại số và Giải tích 11 Nâng cao