Logo

Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao

Tổng quan nội dung

Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học.

Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, tập xác định và tập giá trị để giải quyết.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài.

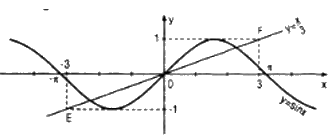
Chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình với đồ thị của hàm số y = sinx đều cách gốc tọa độ một khoảng nhỏ hơn

Đề bài

Chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình \(y = {x \over 3}\) với đồ thị của hàm số \(y = \sin x\) đều cách gốc tọa độ một khoảng nhỏ hơn \(\sqrt {10} \)

Lời giải chi tiết

Đường thẳng \(y = {x \over 3}\) đi qua các điểm \(E(-3 ; -1)\) và \(F(3 ; 1)\)

Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao 1

Chỉ có đoạn thẳng \(EF\) của đường thẳng đó nằm trong dải \(\left\{ {\left( {x{\rm{ }};{\rm{ }}y} \right)| - 1{\rm{ }} \le {\rm{ }}y{\rm{ }} \le {\rm{ }}1} \right\}\) (dải này chứa đồ thị của hàm số \(y = \sin x\)).

Vậy các giao điểm của đường thẳng \(y = {x \over 3}\) với đồ thị của hàm số \(y = \sin x\) phải thuộc đoạn \(EF\).

Mọi điểm của đoạn thẳng này cách \(O\) một khoảng không dài hơn \(OE=OF=\sqrt {3^2 + 1^2} = \sqrt {10} \)

Rõ ràng \(E, F\) không thuộc đồ thị của hàm số \(y = \sin x\) nên khoảng cách từ các giao điểm đến O nhỏ hơn \(\sqrt {10}\).

Giải Chi Tiết Câu 10 Trang 17 SGK Đại Số và Giải Tích 11 Nâng Cao

Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao thuộc chương trình học về hàm số. Để giải quyết bài tập này, học sinh cần nắm vững các khái niệm cơ bản như tập xác định, tập giá trị, và cách xác định hàm số.

Nội Dung Bài Tập

Bài tập yêu cầu xác định tập xác định của hàm số cho trước. Thông thường, hàm số có thể là một biểu thức đại số, một phân thức, hoặc một hàm số phức tạp hơn. Việc xác định tập xác định đòi hỏi học sinh phải xem xét các điều kiện để hàm số có nghĩa, ví dụ như mẫu số khác 0, căn thức phải không âm, hoặc logarit phải có cơ số lớn hơn 0 và khác 1.

Phương Pháp Giải

  1. Xác định dạng hàm số: Phân loại hàm số (đa thức, phân thức, căn thức, logarit, mũ...).
  2. Tìm điều kiện xác định: Xác định các điều kiện để hàm số có nghĩa. Ví dụ:
    • Với phân thức: Mẫu số khác 0.
    • Với căn thức: Biểu thức dưới dấu căn lớn hơn hoặc bằng 0.
    • Với logarit: Cơ số lớn hơn 0 và khác 1, biểu thức trong logarit lớn hơn 0.
  3. Giải các bất phương trình/phương trình: Giải các bất phương trình hoặc phương trình để tìm ra miền giá trị của biến số thỏa mãn điều kiện xác định.
  4. Kết luận: Viết tập xác định của hàm số dưới dạng khoảng, nửa khoảng, hoặc tập hợp.

Ví Dụ Minh Họa

Giả sử hàm số được cho là: f(x) = √(x - 2) / (x + 1)

Để xác định tập xác định, ta cần thỏa mãn hai điều kiện:

  • x - 2 ≥ 0 => x ≥ 2
  • x + 1 ≠ 0 => x ≠ -1

Kết hợp hai điều kiện trên, ta có tập xác định của hàm số là: [2, +∞)

Lưu Ý Quan Trọng

  • Luôn kiểm tra kỹ các điều kiện xác định để tránh sai sót.
  • Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm toán học để kiểm tra lại kết quả.
  • Luyện tập thường xuyên với nhiều dạng bài tập khác nhau để nắm vững kiến thức.

Tại Sao Nên Chọn tusach.vn?

tusach.vn cung cấp:

  • Lời giải chi tiết, dễ hiểu, được trình bày rõ ràng.
  • Đội ngũ giáo viên giàu kinh nghiệm, luôn sẵn sàng hỗ trợ học sinh.
  • Cập nhật liên tục các bài giải mới nhất, theo sát chương trình học.
  • Giao diện thân thiện, dễ sử dụng.

Bài Tập Tương Tự

Để củng cố kiến thức, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Đại số và Giải tích 11 Nâng cao, hoặc trên các trang web học tập trực tuyến khác.

Kết Luận

Việc nắm vững phương pháp giải Câu 10 trang 17 SGK Đại số và Giải tích 11 Nâng cao là rất quan trọng để học tốt môn Toán. Hãy luyện tập thường xuyên và đừng ngần ngại tìm kiếm sự giúp đỡ khi gặp khó khăn. tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức!