Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Câu 29 trang 211 SGK Đại số và Giải tích 11 Nâng cao
SGK Toán 11 Nâng cao
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
CHƯƠNG V. ĐẠO HÀM
Bài 3. Đạo hàm của các hàm số lượng giác

Câu 29 trang 211 SGK Đại số và Giải tích 11 Nâng cao

Câu 29 trang 211 SGK Đại số và Giải tích 11 Nâng cao

Bài tập này thuộc chương trình Đại số và Giải tích 11 Nâng cao, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến...

Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và phương pháp giải bài tập hiệu quả.

Hãy cùng tusach.vn khám phá lời giải của Câu 29 trang 211 ngay bây giờ!

Tìm đạo hàm của các hàm số sau :

LG aLG bLG cLG dLG eLG f

LG a

    \(y = 5\sin x - 3\cos x\)

    Phương pháp giải:

    Sử dụng các công thức (sinx)'=cosx và (cosx)'=-sinx.

    Lời giải chi tiết:

    \(y' = 5\cos x + 3\sin x\)

    LG b

       \(y = \sin \left( {{x^2} - 3x + 2} \right)\)

      Phương pháp giải:

      Sử dụng công thức (sinu)'=u'cosu

      Lời giải chi tiết:

      \(y'=\left[ {\sin \left( {{x^2} - 3x + 2} \right)} \right]' \) \(= \left( {{x^2} - 3x + 2} \right)'\cos \left( {{x^2} - 3x + 2} \right)\) \(= \left( {2x - 3} \right)\cos \left( {{x^2} - 3x + 2} \right)\)

      LG c

         \(y = \cos \sqrt {2x + 1} \)

        Phương pháp giải:

        Sử dụng công thức (cosu)'=-u'sinu

        Lời giải chi tiết:

        \(y' = - \left( {\sqrt {2x + 1} } \right)'\sin \sqrt {2x + 1}\) \( = - \frac{{\left( {2x + 1} \right)'}}{{2\sqrt {2x + 1} }}\sin \sqrt {2x + 1} \) \(= -{2 \over {2\sqrt {2x + 1} }}\left( { \sin \sqrt {2x + 1} } \right)\) \( = {{ - \sin \sqrt {2x + 1} } \over {\sqrt {2x + 1} }}\)

        LG d

          \(y = 2\sin 3x\cos 5x\)

          Phương pháp giải:

          Biến đổi tích thành tổng và tính đạo hàm.

          Lời giải chi tiết:

          \(y = 2.\frac{1}{2}\left[ {\sin \left( {3x + 5x} \right) + \sin \left( {3x - 5x} \right)} \right] \) \(= \sin 8x + \sin \left( { - 2x} \right)\) \(= \sin 8x - \sin 2x \) \(\Rightarrow y' = \left( {8x} \right)'\cos 8x - \left( {2x} \right)'\cos 2x\) \(= 8\cos 8x - 2\cos 2x\)

          LG e

            \(y = {{\sin x + \cos x} \over {\sin x - \cos x}}\)

            Phương pháp giải:

            Sử dụng công thức đạo hàm của một thương \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\)

            Lời giải chi tiết:

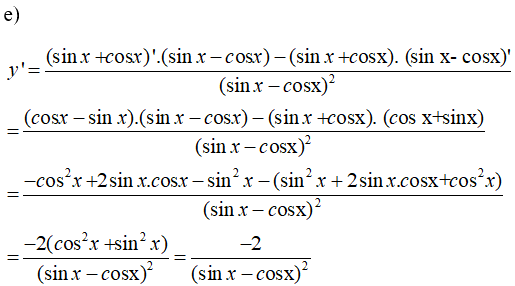
            Câu 29 trang 211 SGK Đại số và Giải tích 11 Nâng cao 1

            LG f

              \(y = \sqrt {\cos 2x} \)

              Phương pháp giải:

              Sử dụng công thức \(\left( {\sqrt u } \right)' = \frac{{u'}}{{2\sqrt u }}\)

              Lời giải chi tiết:

              \(y' = \frac{{\left( {\cos 2x} \right)'}}{{2\sqrt {\cos 2x} }} = \frac{{\left( {2x} \right)'.\left( { - \sin 2x} \right)}}{{2\sqrt {\cos 2x} }}\) \(= {{ - 2\sin 2x} \over {2\sqrt {\cos 2x} }} = {-{\sin 2x} \over {\sqrt {\cos 2x} }}\)

              Giải Chi Tiết Câu 29 Trang 211 SGK Đại số và Giải tích 11 Nâng cao

              Câu 29 trang 211 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về... (nêu rõ kiến thức liên quan, ví dụ: hàm số, đạo hàm, tích phân, véc tơ, hình học không gian,...). Bài viết này sẽ cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ cách tiếp cận và giải quyết bài toán này.

              Đề Bài Câu 29 Trang 211 SGK Đại số và Giải tích 11 Nâng cao

              (Viết lại đầy đủ đề bài ở đây)

              Lời Giải Chi Tiết

              Để giải Câu 29 trang 211, chúng ta cần thực hiện các bước sau:

              1. Bước 1: Phân tích đề bài và xác định yêu cầu của bài toán.
              2. Bước 2: Áp dụng các kiến thức và công thức liên quan để xây dựng phương án giải.
              3. Bước 3: Thực hiện các phép tính và biến đổi đại số cần thiết.
              4. Bước 4: Kiểm tra lại kết quả và đảm bảo tính chính xác.

              Giải:

              (Giải bài toán chi tiết, trình bày rõ ràng từng bước. Sử dụng các ký hiệu toán học và giải thích rõ ràng các bước thực hiện.)

              Ví Dụ Minh Họa

              Để giúp bạn hiểu rõ hơn về cách giải, chúng ta sẽ xem xét một ví dụ minh họa tương tự:

              (Đưa ra một ví dụ tương tự và giải chi tiết)

              Lưu Ý Quan Trọng

              • Luôn đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
              • Sử dụng các công thức và định lý một cách chính xác.
              • Kiểm tra lại kết quả để đảm bảo tính chính xác.
              • Luyện tập thường xuyên để nâng cao kỹ năng giải toán.

              Các Bài Tập Tương Tự

              Để củng cố kiến thức và kỹ năng, bạn có thể tham khảo các bài tập tương tự sau:

              • Bài tập 1: (Đề bài)
              • Bài tập 2: (Đề bài)
              • Bài tập 3: (Đề bài)

              Tổng Kết

              Câu 29 trang 211 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng, giúp bạn rèn luyện kỹ năng giải toán và củng cố kiến thức về... (nêu lại kiến thức liên quan). Hy vọng với lời giải chi tiết và ví dụ minh họa trong bài viết này, bạn đã hiểu rõ cách tiếp cận và giải quyết bài toán này một cách hiệu quả.

              Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại để lại bình luận bên dưới. tusach.vn luôn sẵn sàng hỗ trợ bạn!

              Bảng Tham Khảo (nếu cần)

              Công thứcMô tả
              (Công thức 1)(Mô tả công thức 1)
              (Công thức 2)(Mô tả công thức 2)

              Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

              CHỦ ĐỀ SÁCH XEM NHIỀU

              Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

              VỀ TUSACH.VN