Câu 18 trang 55 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 18 Trang 55 SGK Hình Học 11 Nâng Cao
Câu 18 trang 55 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian lớp 11. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng, mối quan hệ giữa chúng, và các định lý liên quan để giải quyết.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, cùng với phương pháp giải bài toán này, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tứ diện ABCD. Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AB; P, Q là hai điểm phân biệt cùng thuộc đường thẳng CD. Xét vị trí tương đối của hai đường thẳng MQ, NP và vị trí tương đối của hai đường thẳng MP, NQ
Đề bài
Cho tứ diện ABCD. Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AB; P, Q là hai điểm phân biệt cùng thuộc đường thẳng CD. Xét vị trí tương đối của hai đường thẳng MQ, NP và vị trí tương đối của hai đường thẳng MP, NQ
Lời giải chi tiết
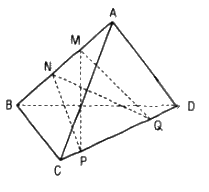
Hai đường thẳng MQ và NP chéo nhau.
Thật vậy, giả sử chúng không chéo nhau, tức chúng cùng thuộc một mp(\(\alpha\)) nào đó. Vậy M, N, P, Q cùng thuộc mp(\(\alpha\)) và do đó A, B, C, D cùng thuộc mp(\(\alpha\)). Điều này mâu thuẫn với giả thiết ABCD là một tứ diện.
Chứng minh tương tự, hai đường thẳng MP và NQ cũng chéo nhau.
Giải Chi Tiết Câu 18 Trang 55 SGK Hình Học 11 Nâng Cao
Câu 18 trang 55 SGK Hình học 11 Nâng cao thường xoay quanh các bài toán liên quan đến việc xác định mối quan hệ giữa đường thẳng và mặt phẳng, hoặc giữa hai mặt phẳng. Để giải quyết những bài toán này, học sinh cần nắm vững các kiến thức cơ bản sau:
- Đường thẳng song song với mặt phẳng: Một đường thẳng song song với mặt phẳng nếu nó không có điểm chung với mặt phẳng đó.
- Đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với mặt phẳng nếu nó tạo với mặt phẳng một góc vuông.
- Hai mặt phẳng song song: Hai mặt phẳng song song nếu chúng không có điểm chung.
- Hai mặt phẳng vuông góc: Hai mặt phẳng vuông góc nếu góc giữa chúng bằng 90 độ.
Phân Tích Đề Bài và Lập Kế Hoạch Giải
Trước khi bắt tay vào giải bài toán, điều quan trọng là phải đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lập kế hoạch giải bằng cách:
- Vẽ hình minh họa (nếu cần thiết).
- Xác định các mối quan hệ giữa các yếu tố đã cho.
- Sử dụng các định lý, tính chất liên quan để chứng minh hoặc tính toán.
Lời Giải Chi Tiết (Ví dụ minh họa - cần thay thế bằng lời giải cụ thể của câu 18 trang 55)
Đề bài (Ví dụ): Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Lời giải:
- Vì SA vuông góc với mặt phẳng (ABCD) nên SA vuông góc với SC.
- Do đó, tam giác SAC vuông tại S.
- Góc giữa đường thẳng SC và mặt phẳng (ABCD) chính là góc SCA.
- Trong tam giác SAC vuông tại S, ta có: tan SCA = SA/AC = a/(a√2) = 1/√2.
- Suy ra, SCA = arctan(1/√2) ≈ 35.26 độ.
Các Dạng Bài Tập Tương Tự và Phương Pháp Giải
Ngoài câu 18 trang 55, còn rất nhiều bài tập tương tự trong SGK Hình học 11 Nâng cao. Để giải tốt các bài tập này, học sinh nên:
- Luyện tập thường xuyên các bài tập về đường thẳng và mặt phẳng.
- Nắm vững các định lý, tính chất liên quan.
- Rèn luyện kỹ năng vẽ hình và phân tích đề bài.
Mở Rộng Kiến Thức
Kiến thức về đường thẳng và mặt phẳng có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, và thiết kế. Việc hiểu rõ các khái niệm và định lý liên quan sẽ giúp học sinh có cái nhìn sâu sắc hơn về thế giới xung quanh.
Bảng Tổng Hợp Các Công Thức Liên Quan
| Công thức | Mô tả |
|---|---|
| d(A, (P)) | Khoảng cách từ điểm A đến mặt phẳng (P) |
| cos(θ) | Góc giữa đường thẳng d và mặt phẳng (P) |
Hy vọng với lời giải chi tiết và những kiến thức bổ ích trên, các em học sinh sẽ tự tin hơn khi giải Câu 18 trang 55 SGK Hình học 11 Nâng cao và các bài tập tương tự. Chúc các em học tốt!