Giải bài 9 trang 95 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 9 trang 95 SBT Toán 11 Cánh Diều
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 9 trang 95 sách bài tập Toán 11 Cánh Diều. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất.
Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng cần thiết để tự tin giải quyết các bài toán tương tự.
Cho hình chóp tứ giác \(S.ABCD\) có đáy không là hình thang. Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Trên \(SO\) lấy điểm \(I\) sao cho \(SI = 2IO\).
Đề bài
Cho hình chóp tứ giác \(S.ABCD\) có đáy không là hình thang. Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Trên \(SO\) lấy điểm \(I\) sao cho \(SI = 2IO\).
a) Xác định các giao điểm \(M\), \(N\) lần lượt của \(SA\), \(SD\) với mặt phẳng \(\left( {IBC} \right)\).
b*) Chứng minh rằng các đường thẳng \(AD\), \(BC\) và \(MN\) đồng quy.
Phương pháp giải - Xem chi tiết
a) Để xác định giao điểm của mặt phẳng với một đường thẳng cho trước, ta cần chọn một đường thẳng khác nằm trong mặt phẳng đã cho, rồi tìm giao điểm của 2 đường thẳng đó.
b) Gọi \(K\) là giao điểm của \(AD\) và \(BC\). Ta cần chứng minh \(MN = \left( {IBC} \right) \cap \left( {SAD} \right)\). Từ đó suy ra \(K \in MN\).
Lời giải chi tiết
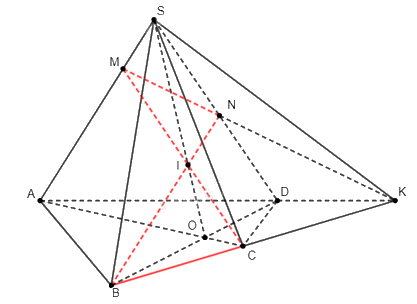
a)
Giao điểm \(M\) của \(SA\) và \(\left( {IBC} \right)\):
Ta nhận xét rằng \(I \in SO \subset \left( {SAC} \right) \Rightarrow CI \subset \left( {SAC} \right)\).
Trên mặt phẳng \(\left( {SAC} \right)\), gọi \(\left\{ M \right\} = CI \cap SA\).
Do \(IC \subset \left( {IBC} \right)\), nên \(\left\{ M \right\} = \left( {IBC} \right) \cap SA\).
Vậy \(M\) là giao điểm của \(\left( {IBC} \right)\) và \(SA\).
Giao điểm \(N\) của \(SD\) và \(\left( {IBC} \right)\):
Ta nhận xét rằng \(I \in SO \subset \left( {SBD} \right) \Rightarrow BI \subset \left( {SBD} \right)\).
Trên mặt phẳng \(\left( {SBD} \right)\), gọi \(\left\{ N \right\} = BI \cap SD\).
Do \(IB \subset \left( {IBC} \right)\), nên \(\left\{ N \right\} = \left( {IBC} \right) \cap SD\).
Vậy \(N\) là giao điểm của \(\left( {IBC} \right)\) và \(SD\).
b) Trên mặt phẳng \(\left( {ABCD} \right)\), gọi \(K\) là giao điểm của \(AD\) và \(BC\).
Ta có \(\left\{ \begin{array}{l}M \in SA \subset \left( {SAD} \right)\\M \in \left( {IBC} \right)\end{array} \right. \Rightarrow M \in \left( {SAD} \right) \cap \left( {IBC} \right)\).
Mặt khác, \(\left\{ \begin{array}{l}N \in SD \subset \left( {SAD} \right)\\N \in \left( {IBC} \right)\end{array} \right. \Rightarrow N \in \left( {SAD} \right) \cap \left( {IBC} \right)\).
Vậy giao tuyến của \(\left( {SAD} \right)\) và \(\left( {IBC} \right)\) là đường thẳng \(MN\).
Do \(AD \in \left( {SAD} \right)\), \(BC \in \left( {IBC} \right)\), \(\left\{ K \right\} = AD \cap BC\), ta suy ra \(K\) nằm trên giao tuyến của \(\left( {SAD} \right)\) và \(\left( {IBC} \right)\), tức là \(K \in MN\).
Vậy ba đường thẳng \(AD\), \(BC\), \(MN\) cắt nhau tại \(K\).
Giải bài 9 trang 95 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải
Bài 9 trang 95 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về hàm số lượng giác và đồ thị. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về các phép biến đổi lượng giác, tính chất của hàm số lượng giác và sử dụng đồ thị để giải quyết các bài toán thực tế.
Nội dung chính của bài 9 trang 95 SBT Toán 11 Cánh Diều
- Phần 1: Bài tập về việc xác định tập xác định của hàm số lượng giác.
- Phần 2: Bài tập về việc tìm tập giá trị của hàm số lượng giác.
- Phần 3: Bài tập về việc xét tính chẵn lẻ của hàm số lượng giác.
- Phần 4: Bài tập về việc vẽ đồ thị hàm số lượng giác.
Hướng dẫn giải chi tiết bài 9 trang 95 SBT Toán 11 Cánh Diều
Để giải quyết bài 9 trang 95 SBT Toán 11 Cánh Diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Các phép biến đổi lượng giác cơ bản: Cộng, trừ, nhân, chia góc; công thức lượng giác cơ bản.
- Tính chất của hàm số lượng giác: Chu kỳ, tính chẵn lẻ, giá trị lớn nhất, giá trị nhỏ nhất.
- Cách vẽ đồ thị hàm số lượng giác: Xác định các điểm đặc biệt, vẽ đồ thị dựa trên các điểm đó.
Ví dụ minh họa giải bài 9 trang 95 SBT Toán 11 Cánh Diều (một phần)
Bài 9.1: Xác định tập xác định của hàm số y = tan(2x + π/3).
Lời giải:
Hàm số y = tan(2x + π/3) xác định khi và chỉ khi 2x + π/3 ≠ π/2 + kπ (k ∈ Z).
Suy ra 2x ≠ π/2 + kπ - π/3 = π/6 + kπ (k ∈ Z).
Vậy x ≠ π/12 + kπ/2 (k ∈ Z).
Tập xác định của hàm số là D = R \ {π/12 + kπ/2 | k ∈ Z}.
Mẹo giải nhanh bài tập Toán 11 Cánh Diều
- Sử dụng máy tính bỏ túi: Để tính toán nhanh các giá trị lượng giác.
- Vẽ phác đồ thị: Để hình dung rõ hơn về hàm số.
- Kiểm tra lại kết quả: Để đảm bảo tính chính xác.
Tại sao nên chọn tusach.vn để giải bài tập Toán 11 Cánh Diều?
tusach.vn cung cấp:
- Lời giải chi tiết, dễ hiểu: Được trình bày bởi đội ngũ giáo viên giàu kinh nghiệm.
- Đáp án chính xác: Đảm bảo tính tin cậy.
- Giao diện thân thiện: Dễ dàng tìm kiếm và sử dụng.
- Cập nhật liên tục: Đáp ứng nhu cầu học tập của học sinh.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác và nâng cao kết quả học tập của bạn!
Bảng tổng hợp các công thức lượng giác thường dùng
| Công thức | Mô tả |
|---|---|
| sin2x + cos2x = 1 | Công thức lượng giác cơ bản |
| tan x = sin x / cos x | Định nghĩa hàm tan |
| cot x = cos x / sin x | Định nghĩa hàm cot |