Giải bài 74 trang 33 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 74 trang 33 SBT Toán 11 Cánh Diều
Tusach.vn xin giới thiệu đáp án chi tiết bài 74 trang 33 sách bài tập Toán 11 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải SBT Toán 11 Cánh Diều, đáp ứng nhu cầu học tập của học sinh.
Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm.
Đề bài
Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm. Khoảng cách \(h\) (cm) từ chất điểm đến trục hoành được tính theo công thức \(h = \left| y \right|\), trong đó \(y = a\sin \left( {\frac{\pi }{5}t} \right)\), với \(t\) là thời gian chuyển động của chất điểm tính bằng giây \(\left( {t \ge 0} \right)\) và chất điểm bắt đầu chuyển động từ vị trí \(A\) (Xem hình dưới)
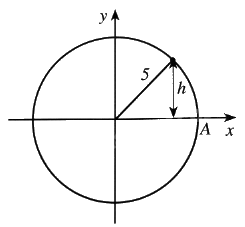
a) Chất điểm chuyển động một vòng hết bao nhiêu giây?
b) Tìm giá trị của \(a\).
c) Tìm thời điểm sao cho chất điểm ở vị trí có \(h = 2,5\) cm và nằm phía dưới trục hoành trong một vòng quay đầu tiên.
Phương pháp giải - Xem chi tiết
a) Thời gian chất điểm chuyển động một vòng là chu kì của chất điểm đó.
Xét \(h = 0 \Leftrightarrow y = 0 \Leftrightarrow \sin \left( {\frac{\pi }{5}t} \right) = 0 \Leftrightarrow t = 5k\)\(\left( {k \in \mathbb{Z}} \right)\)
Nhận thấy \(k = 2\), ta thấy chất điểm và quay về vị trí\(A\). Do vậy, thời gian chất điểm chuyển động một vòng là 10 giây.
b) Do thời gian chất điểm chuyển động một vòng là 10 giây, nên sau 2,5 giây chất điểm chuyển động được một phần tư vòng tròn theo chiều dương. Như vậy tại \(t = 2,5\) ta có: \(a\sin \left( {\frac{\pi }{5}.\frac{5}{2}} \right) = 5 \Leftrightarrow a = 5\).
c) Yêu cầu đề bài tương đương với việc tìm \(t\) để \(y = 5\sin \left( {\frac{\pi }{5}t} \right) = - 2,5\).
Giải phương trình ẩn \(t\) và kết luận.
Lời giải chi tiết
a) Thời gian chất điểm chuyển động một vòng là chu kì của chất điểm đó.
Xét \(t = 0 \Rightarrow h = 0\), ta thấy chất điểm ở vị trí \(A\). Ta cần tìm thời gian gần nhất kể từ thời điểm \(t = 0\) (giây), chất điểm lại quay về vị trí \(A\).
Xét \(h = 0 \Leftrightarrow y = 0 \Leftrightarrow \sin \left( {\frac{\pi }{5}t} \right) = 0 \Leftrightarrow t = 5k\)\(\left( {k \in \mathbb{Z}} \right)\)
Với \(k = 1\), ta thấy chất điểm chuyển động được nửa vòng tròn.
Với \(k = 2\), ta thấy chất điểm chuyển động được một vòng tròn, và quay về vị trí\(A\).
Do vậy, thời gian chất điểm chuyển động một vòng là 10 giây.
b) Do thời gian chất điểm chuyển động một vòng là 10 giây, nên sau 2,5 giây chất điểm chuyển động được một phần tư vòng tròn theo chiều dương. Như vậy tại \(t = 2,5\) ta có: \(y = \left| y \right| = h = 5 \Leftrightarrow a\sin \left( {\frac{\pi }{5}.\frac{5}{2}} \right) = 5 \Leftrightarrow a\sin \left( {\frac{\pi }{2}} \right) = 5 \Leftrightarrow a = 5\).
\( \Rightarrow y = 5\sin \left( {\frac{\pi }{5}t} \right)\)
c) Ta cần tìm \(t\) để \(h = 2,5\)cm và ở dưới trục hoành nên \(y = - 2,5\).
\(5\sin \left( {\frac{\pi }{5}t} \right) = - 2,5 \Leftrightarrow \sin \left( {\frac{\pi }{5}t} \right) = - \frac{1}{2}\)
Ta thấy \(\sin \frac{{ - \pi }}{6} = - \frac{1}{2}\), phương trình ở trên tương đương với
\(\sin \left( {\frac{\pi }{5}t} \right) = \sin \frac{{ - \pi }}{6} \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{5}t = - \frac{\pi }{6} + k2\pi \\\frac{\pi }{5}t = \pi + \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = \frac{{ - 5 + 60k}}{6}\\t = \frac{{35 + 60k}}{6}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vì ta chỉ xét vòng quay đầu tiên, nên \(0 \le t \le 10\). Do đó \(t = \frac{{35}}{6}\), \(t = \frac{{55}}{6}\)
Vậy tại thời điểm \(t = \frac{{35}}{6}\) giây, \(t = \frac{{55}}{6}\) giây, chất điểm cách trục hoành 2,5 cm và nằm ở dưới trục hoành.
Giải bài 74 trang 33 SBT Toán 11 Cánh Diều: Tổng quan
Bài 74 trang 33 sách bài tập Toán 11 Cánh Diều thuộc chương trình học môn Toán lớp 11, tập trung vào việc vận dụng các kiến thức về vectơ, các phép toán vectơ, và ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh chứng minh đẳng thức vectơ, tìm tọa độ của vectơ, hoặc giải các bài toán liên quan đến hình học sử dụng vectơ.
Nội dung chi tiết bài 74 trang 33 SBT Toán 11 Cánh Diều
Để giải quyết bài 74 trang 33 SBT Toán 11 Cánh Diều một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
- Định nghĩa vectơ: Hiểu rõ khái niệm vectơ, các yếu tố của vectơ (điểm gốc, điểm cuối, độ dài, hướng).
- Các phép toán vectơ: Cộng, trừ, nhân với một số thực vectơ.
- Tọa độ của vectơ: Cách biểu diễn vectơ bằng tọa độ trong hệ tọa độ.
- Ứng dụng của vectơ trong hình học: Chứng minh các tính chất hình học, giải các bài toán về đường thẳng, đường tròn, tam giác,...
Hướng dẫn giải chi tiết bài 74 trang 33 SBT Toán 11 Cánh Diều
Dưới đây là hướng dẫn giải chi tiết từng phần của bài 74 trang 33 SBT Toán 11 Cánh Diều. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, kèm theo các giải thích chi tiết để giúp học sinh hiểu rõ bản chất của bài toán.
Ví dụ minh họa (Giả sử bài 74 có 3 câu a, b, c)
Câu a: (Đề bài cụ thể của câu a). Giải:...
Câu b: (Đề bài cụ thể của câu b). Giải:...
Câu c: (Đề bài cụ thể của câu c). Giải:...
Mẹo giải nhanh bài tập vectơ
Để giải nhanh các bài tập về vectơ, bạn có thể áp dụng một số mẹo sau:
- Sử dụng tính chất của vectơ: Ví dụ, nếu \overrightarrow{AB} = \overrightarrow{CD} thì tứ giác ABCD là hình bình hành.
- Biến đổi vectơ: Sử dụng các phép toán vectơ để biến đổi biểu thức vectơ về dạng đơn giản hơn.
- Sử dụng hệ tọa độ: Chuyển bài toán hình học sang bài toán đại số bằng cách sử dụng hệ tọa độ.
Luyện tập thêm
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, bạn có thể tham khảo thêm các bài tập sau:
- Bài tập tương tự trong sách bài tập Toán 11 Cánh Diều.
- Các bài tập trực tuyến trên các trang web học Toán.
- Các đề thi thử Toán 11.
Kết luận
Bài 74 trang 33 SBT Toán 11 Cánh Diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về vectơ và ứng dụng của vectơ trong hình học. Hy vọng với hướng dẫn chi tiết và các mẹo giải nhanh trên, các bạn học sinh sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các bạn học tốt!
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tọa độ vectơ | Cách biểu diễn vectơ bằng các số trong hệ tọa độ. |
| Nguồn: tusach.vn | |