Giải bài 17 trang 100 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 17 trang 100 SBT Toán 11 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 17 trang 100 sách bài tập Toán 11 Cánh Diều. Bài viết này cung cấp đáp án chính xác, phương pháp giải dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, cập nhật nhanh chóng và đầy đủ nhất để hỗ trợ quá trình học tập của các bạn.
Cho hình chóp tứ giác \(S.ABCD\). Gọi \(G\), \(K\) lần lượt là trọng tâm của các tam giác \(SAB\) và \(SAD\)
Đề bài
Cho hình chóp tứ giác \(S.ABCD\). Gọi \(G\), \(K\) lần lượt là trọng tâm của các tam giác \(SAB\) và \(SAD\); \(M\), \(N\) lần lượt là trung điểm của các cạnh \(BC\) và \(CD\). Chứng minh rằng \(GK\parallel MN\).
Phương pháp giải - Xem chi tiết
Gọi \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(AD\). Chứng minh rằng các đường thẳng \(GK\), \(PQ\), \(BD\), \(MN\) đôi một song song với nhau, từ đó suy ra điều phải chứng minh.
Lời giải chi tiết
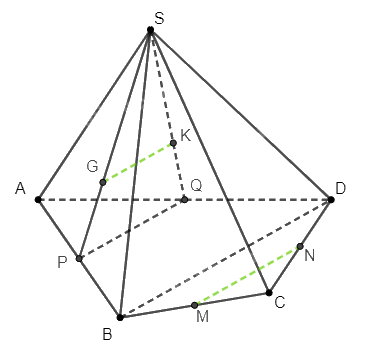
Gọi \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(AD\).
Ta có \(G\) là trọng tâm của tam giác \(SAB\), nên suy ra \(G \in SP\) và \(\frac{{SG}}{{SP}} = \frac{2}{3}\).
Chứng minh tương tự ta cũng có \(K \in SQ\) và \(\frac{{SK}}{{SQ}} = \frac{2}{3}\).
Tam giác \(SPQ\) có \(\frac{{SG}}{{SP}} = \frac{{SK}}{{SQ}}\) nên theo định lí Thales ta có \(GK\parallel PQ\).
Xét tam giác \(ABD\), ta có \(P\) là trung điểm của \(AB\), \(Q\) là trung điểm của \(AD\), nên \(PQ\) là đường trung bình của tam giác \(ABD\). Suy ra \(PQ\parallel BD\).
Chứng minh tương tự ta cũng có \(MN\parallel BD\).
Từ đó suy ra \(GK\parallel MN\). Bài toán được chứng minh.
Giải bài 17 trang 100 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải
Bài 17 trang 100 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về vectơ trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, tích vô hướng, và các tính chất liên quan để giải quyết các bài toán hình học không gian.
Nội dung chi tiết bài 17 trang 100 SBT Toán 11 Cánh Diều
Bài 17 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tính độ dài vectơ, góc giữa hai vectơ.
- Dạng 2: Chứng minh các đẳng thức vectơ.
- Dạng 3: Xác định mối quan hệ giữa các vectơ (cùng phương, vuông góc).
- Dạng 4: Ứng dụng các kiến thức về vectơ để giải các bài toán hình học không gian (ví dụ: tính diện tích, thể tích).
Lời giải chi tiết bài 17 trang 100 SBT Toán 11 Cánh Diều
Để giúp các bạn hiểu rõ hơn về cách giải bài 17, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài tập. Lưu ý rằng, trước khi bắt đầu giải bài tập, các bạn nên ôn lại lý thuyết và các công thức liên quan.
Ví dụ minh họa (Giả định một câu hỏi cụ thể trong bài 17):
Câu hỏi: Cho hai vectơ a = (1; 2; 3) và b = (-2; 1; 0). Tính tích vô hướng của hai vectơ này.
Lời giải:
Tích vô hướng của hai vectơ a và b được tính theo công thức:
a.b = xa.xb + ya.yb + za.zb
Trong đó:
- a = (xa; ya; za)
- b = (xb; yb; zb)
Áp dụng công thức vào bài toán, ta có:
a.b = 1.(-2) + 2.1 + 3.0 = -2 + 2 + 0 = 0
Vậy, tích vô hướng của hai vectơ a và b là 0.
Mẹo giải nhanh và lưu ý quan trọng
Để giải nhanh các bài tập về vectơ, các bạn nên:
- Nắm vững các công thức tính độ dài vectơ, tích vô hướng, tích có hướng.
- Sử dụng các tính chất của các phép toán vectơ để đơn giản hóa bài toán.
- Vẽ hình minh họa để dễ dàng hình dung bài toán.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín
Tusach.vn là địa chỉ tin cậy cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập Toán 11. Chúng tôi luôn cập nhật nội dung mới nhất và đa dạng các dạng bài tập để đáp ứng nhu cầu học tập của các bạn. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
Chúc các bạn học tập tốt!