Giải bài 49 trang 110 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 49 trang 110 SBT Toán 11 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 49 trang 110 sách bài tập Toán 11 Cánh Diều. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những nội dung chất lượng, chính xác và cập nhật nhất để hỗ trợ học sinh trong quá trình học tập.
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông cạnh \(a\)
Đề bài
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình vuông cạnh \(a\), \(AC\) cắt \(BD\) tại \(O\), \(SO \bot \left( {ABCD} \right)\), \(SA = 2a\). Tính khoảng cách:
a) Từ điểm \(A\) đến mặt phẳng \(\left( {SBD} \right)\).
b) Giữa hai đường thẳng \(SO\) và \(CD\).
c) Từ điểm \(O\) đến mặt phẳng \(\left( {SCD} \right)\).
d*) Giữa hai đường thẳng \(AB\) và \(SD\).
Phương pháp giải - Xem chi tiết
a) Chỉ ra rằng \(AO \bot \left( {SBD} \right)\), từ đó suy ra rằng khoảng cách cần tìm là đoạn thẳng \(AO\).
b) Gọi \(M\) là hình chiếu của \(O\) trên \(CD\). Chứng minh rằng \(OM\) là đường vuông góc chung của 2 đường thẳng \(SO\) và \(CD\), từ đó khoảng cách cần tìm là đoạn thẳng \(OM\).
c) Gọi \(H\) là hình chiếu của \(O\) trên \(SM\). Chứng minh rằng \(H\) cũng là hình chiếu của \(O\) trên \(\left( {SCD} \right)\), từ đó suy ra khoảng cách cần tìm là đoạn thẳng \(OH\).
d) Gọi \(G\) là hình chiếu của \(A\) trên \(\left( {SCD} \right)\). Chỉ ra rằng \(AB\parallel \left( {SCD} \right)\) và \(SD \subset \left( {SCD} \right)\) nên khoảng cách giữa \(AB\) và \(SD\) cũng chính là khoảng cách giữa \(AB\) và \(\left( {SCD} \right)\), và bằng \(AG\). Sử dụng định lí Thales để tính \(AG\).
Lời giải chi tiết
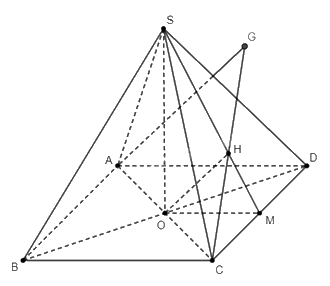
a) Ta có \(ABCD\) là hình vuông, nên \(AO \bot BD\). Hơn nữa, do \(SO \bot \left( {ABCD} \right)\) nên \(SO \bot AO\). Như vậy, do \(AO \bot BD\), \(SO \bot AO\) nên \(AO \bot \left( {SBD} \right)\). Điều này có nghĩa \(O\) là hình chiếu của \(A\) trên \(\left( {SBD} \right)\). Vậy khoảng cách từ \(A\) đến \(\left( {SBD} \right)\) là đoạn thẳng \(AO\).
Ta có \(ABCD\) là hình vuông cạnh \(a\), nên \(AC = a\sqrt 2 \Rightarrow AO = \frac{{a\sqrt 2 }}{2}\).
Vậy khoảng cách từ \(A\) đến \(\left( {SBD} \right)\) là \(\frac{{a\sqrt 2 }}{2}\).
b) Gọi \(M\) là hình chiếu của \(O\) trên \(CD\). Do \(O\) là tâm của hình vuông \(ABCD\) cạnh \(a\), nên ta suy ra \(OM \bot CD\) và \(OM = \frac{a}{2}\).
Do \(SO \bot \left( {ABCD} \right)\), ta suy ra \(SO \bot OM\).
Như vậy, do \(OM \bot CD\), \(SO \bot OM\), nên \(OM\) là đường vuông góc chung của 2 đường thẳng \(SO\) và \(CD\), điều này có nghĩa khoảng cách giữa 2 đường thẳng \(SO\) và \(CD\) là đoạn thẳng \(OM\).
Do \(OM = \frac{a}{2}\), ta kết luận rằng khoảng cách giữa 2 đường thẳng \(SO\) và \(CD\) là \(\frac{a}{2}\).
c) Gọi \(H\) là hình chiếu của \(O\) trên \(SM\). Vì \(SO \bot \left( {ABCD} \right)\) nên \(SO \bot CD\), mà \(OM \bot CD\) nên \(\left( {SOM} \right) \bot CD\), điều này suy ra \(OH \bot CD\). Mà lại có \(OH \bot SM\) nên \(OH \bot \left( {SCD} \right)\).
Vậy \(H\) là hình chiếu của \(O\) trên \(\left( {SCD} \right)\), tức là khoảng cách từ \(O\) đến \(\left( {SCD} \right)\) là đoạn thẳng \(OH\).
Tam giác \(SAO\) vuông tại \(O\) nên \(S{O^2} = S{A^2} - A{O^2} = {\left( {2a} \right)^2} - {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = \frac{{7{a^2}}}{2}\).
Tam giác \(SOM\) vuông tại \(O\) có đường cao \(OH\), nên ta có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{M^2}}} = \frac{2}{{7{a^2}}} + \frac{4}{{{a^2}}} = \frac{{30}}{{7{a^2}}} \Rightarrow OH = \sqrt {\frac{{7{a^2}}}{{30}}} = \frac{{a\sqrt {210} }}{{30}}\).
d) Gọi \(G\) là hình chiếu của \(A\) trên \(\left( {SCD} \right)\).
Ta có \(AB\parallel CD\) nên \(AB\parallel \left( {SCD} \right)\), mà \(SD \subset \left( {SCD} \right)\), nên khoảng cách giữa 2 đường thẳng \(AB\) và \(SD\) cũng bằng khoảng cách giữa \(AB\) và \(\left( {SCD} \right)\), và bằng khoảng cách từ \(A\) đến \(\left( {SCD} \right)\). Do \(G\) là hình chiếu của \(A\) trên \(\left( {SCD} \right)\), nên khoảng cách cần tìm là đoạn thẳng \(AG\).
Do \(OH \bot \left( {SCD} \right)\), \(AG \bot \left( {SCD} \right)\) nên \(OH\parallel AG\).
Tam giác \(ACG\) có \(OH\parallel AG\), nên theo định lí Thales ta có \(\frac{{OH}}{{AG}} = \frac{{CO}}{{CA}} = \frac{1}{2}\).
Suy ra \(AG = 2OH\). Mà \(OH = \frac{{a\sqrt {210} }}{{30}}\) nên \(AG = \frac{{a\sqrt {210} }}{{15}}\).
Giải bài 49 trang 110 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải
Bài 49 trang 110 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng để giải quyết các bài toán thực tế.
Nội dung bài tập 49 trang 110 SBT Toán 11 Cánh Diều
Bài tập 49 thường bao gồm các dạng câu hỏi sau:
- Xác định mối quan hệ giữa đường thẳng và mặt phẳng (song song, vuông góc, cắt nhau).
- Chứng minh một đường thẳng vuông góc với một mặt phẳng.
- Tính góc giữa đường thẳng và mặt phẳng.
- Tìm giao điểm của đường thẳng và mặt phẳng.
Lời giải chi tiết bài 49 trang 110 SBT Toán 11 Cánh Diều
Để giải bài 49 trang 110 SBT Toán 11 Cánh Diều một cách hiệu quả, bạn cần:
- Nắm vững kiến thức lý thuyết: Hiểu rõ các định lý, tính chất về quan hệ giữa đường thẳng và mặt phẳng.
- Phân tích đề bài: Xác định rõ các yếu tố đã cho và yêu cầu của bài toán.
- Vẽ hình: Vẽ hình minh họa giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Sử dụng các công cụ hỗ trợ: Sử dụng thước, compa, máy tính bỏ túi để thực hiện các phép tính và vẽ hình chính xác.
Dưới đây là lời giải chi tiết cho từng phần của bài tập 49 (ví dụ, giả sử bài tập yêu cầu chứng minh một đường thẳng vuông góc với một mặt phẳng):
Ví dụ minh họa: Chứng minh đường thẳng d vuông góc với mặt phẳng (P)
Để chứng minh d ⊥ (P), ta cần chứng minh d vuông góc với mọi đường thẳng nằm trong (P). Cụ thể:
- Chọn hai đường thẳng phân biệt a và b nằm trong (P) sao cho chúng cắt nhau tại một điểm.
- Chứng minh d ⊥ a và d ⊥ b.
- Kết luận d ⊥ (P) theo dấu hiệu nhận biết.
Mẹo giải nhanh bài tập về đường thẳng và mặt phẳng
Để giải nhanh các bài tập về đường thẳng và mặt phẳng, bạn có thể áp dụng một số mẹo sau:
- Sử dụng các định lý đảo để chứng minh các mối quan hệ.
- Tận dụng các tính chất đối xứng của hình học không gian.
- Chia nhỏ bài toán lớn thành các bài toán nhỏ hơn để dễ dàng giải quyết.
Luyện tập thêm
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, bạn nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Tusach.vn cung cấp đầy đủ các bài giải chi tiết và đáp án chính xác cho tất cả các bài tập trong sách bài tập Toán 11 Cánh Diều.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn là website học tập trực tuyến uy tín, cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và đáp án chính xác cho các môn học từ lớp 6 đến lớp 12. Chúng tôi luôn cố gắng tạo ra một môi trường học tập thân thiện, hiệu quả và giúp học sinh đạt được kết quả tốt nhất.
| Chương | Bài | Liên kết |
|---|---|---|
| Chương 3 | Bài 48 | Giải bài 48 trang 110 |
| Chương 3 | Bài 50 | Giải bài 50 trang 112 |