Giải bài 55 trang 118 Toán 11 Cánh Diều - Chi tiết, nhanh chóng

Giải bài 55 trang 118 sách bài tập toán 11 - Cánh diều

Giải bài 55 trang 118 sách bài tập Toán 11 Cánh Diều

Chào mừng các em học sinh đến với lời giải chi tiết bài 55 trang 118 SBT Toán 11 Cánh Diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về nội dung bài học.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.

Cho tứ diện \(ABCD\). Trên cạnh \(CD\) lấy hai điểm \(M\) và \(N\) khác nhau

Đề bài

Cho tứ diện \(ABCD\). Trên cạnh \(CD\) lấy hai điểm \(M\) và \(N\) khác nhau. Chứng minh rằng các đường thẳng \(AM\) và \(BN\) không cắt nhau.

Phương pháp giải - Xem chi tiết Giải bài 55 trang 118 sách bài tập toán 11 - Cánh diều 1

Chứng minh bằng phương pháp “phản chứng”: Giả sử \(AM\) cắt \(BN\), ta sẽ chứng minh được \(A\), \(B\), \(C\), \(D\) đồng phẳng, và đây là điều vô lí. Từ đó suy ra điều phải chứng minh.

Lời giải chi tiết

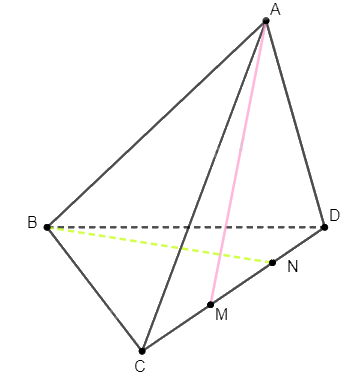
Giải bài 55 trang 118 sách bài tập toán 11 - Cánh diều 2

Giả sử \(AM\) cắt \(BN\). Như vậy tồn tại mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(AM\) và \(BN\).

Do \(M\) và \(N\) cùng nằm trên \(\left( P \right)\), ta suy ra đường thẳng \(MN\) cũng nằm trên \(\left( P \right)\). Từ đó \(C\) và \(D\) cũng thuộc \(\left( P \right)\).

Như vậy \(A\), \(B\), \(C\), \(D\) cùng thuộc mặt phẳng \(\left( P \right)\). Điều này là vô lí, do với mọi tứ diện \(ABCD\) thì 4 điểm \(A\), \(B\), \(C\), \(D\) luôn không đồng phẳng.

Do đó điều giả sử là sai.

Vậy hai đường thẳng \(AM\) và \(BN\) không cắt nhau.

Giải bài 55 trang 118 sách bài tập Toán 11 Cánh Diều: Tổng quan

Bài 55 trang 118 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về Đường thẳng và mặt phẳng trong không gian. Bài tập này thường tập trung vào việc vận dụng kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng, các tính chất của đường thẳng và mặt phẳng song song, và các định lý liên quan.

Nội dung bài tập 55 trang 118 SBT Toán 11 Cánh Diều

Thông thường, bài 55 sẽ bao gồm các dạng bài tập sau:

Xác định vị trí tương đối giữa đường thẳng và mặt phẳng: Cho một đường thẳng và một mặt phẳng, xác định xem đường thẳng có nằm trong mặt phẳng, song song với mặt phẳng hay cắt mặt phẳng.
Chứng minh sự song song: Chứng minh hai đường thẳng song song, hai mặt phẳng song song, hoặc một đường thẳng song song với một mặt phẳng.
Tính góc: Tính góc giữa đường thẳng và mặt phẳng, hoặc góc giữa hai mặt phẳng.
Ứng dụng thực tế: Giải các bài toán liên quan đến ứng dụng của đường thẳng và mặt phẳng trong không gian.

Phương pháp giải bài tập 55 trang 118 SBT Toán 11 Cánh Diều

Để giải quyết bài tập 55 trang 118 SBT Toán 11 Cánh Diều một cách hiệu quả, các em cần nắm vững các kiến thức sau:

Các định nghĩa và tính chất: Định nghĩa về đường thẳng và mặt phẳng, các tính chất của đường thẳng và mặt phẳng song song, các định lý liên quan.
Các dấu hiệu nhận biết: Dấu hiệu nhận biết hai đường thẳng song song, hai mặt phẳng song song, một đường thẳng song song với một mặt phẳng.
Các công thức tính góc: Công thức tính góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng.
Sử dụng vector: Sử dụng vector để biểu diễn đường thẳng, mặt phẳng và các phép toán liên quan.

Lời giải chi tiết bài 55 trang 118 SBT Toán 11 Cánh Diều (Ví dụ)

Bài 55: (Giả sử đề bài cụ thể là: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD)).

Lời giải:

Vẽ hình: Vẽ hình chóp S.ABCD và các đường thẳng, mặt phẳng liên quan.
Xác định góc cần tính: Góc giữa đường thẳng SC và mặt phẳng (ABCD) chính là góc \(SCA\).
Tính toán: Vì SA vuông góc với (ABCD) nên \(SA \perp AC\). Do đó, tam giác SAC vuông tại A. Ta có \(AC = a\sqrt{2}\) và \(SA = a\). Suy ra \(tan(\angle SCA) = \frac{SA}{AC} = \frac{a}{a\sqrt{2}} = \frac{1}{\sqrt{2}}\). Vậy \(\angle SCA = arctan(\frac{1}{\sqrt{2}})\).
Kết luận: Góc giữa đường thẳng SC và mặt phẳng (ABCD) là \(arctan(\frac{1}{\sqrt{2}})\).

Lưu ý khi giải bài tập

Đọc kỹ đề bài và xác định đúng yêu cầu của bài toán.
Vẽ hình minh họa để dễ dàng hình dung và tìm ra phương pháp giải phù hợp.
Sử dụng các kiến thức và công thức đã học một cách linh hoạt và chính xác.
Kiểm tra lại kết quả để đảm bảo tính đúng đắn.

Tusach.vn – Hỗ trợ học tập Toán 11 hiệu quả

Tusach.vn cung cấp đầy đủ lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong sách bài tập Toán 11 Cánh Diều. Ngoài ra, chúng tôi còn cung cấp các tài liệu học tập khác như lý thuyết, bài tập trắc nghiệm, và các bài giảng video để giúp các em học Toán 11 một cách hiệu quả nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!