Giải bài 45 trang 109, 110 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 45 trang 109, 110 sách bài tập Toán 11 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 45 trang 109, 110 SBT Toán 11 Cánh Diều. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu sắc kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu và cập nhật nhanh chóng nhất.
Cho hình chữ nhật \(ABCD\) có \(AB = 3a\), \(AD = 4a\).
Đề bài
Cho hình chữ nhật \(ABCD\) có \(AB = 3a\), \(AD = 4a\).
a) Khoảng cách từ điểm \(A\) đến đường thẳng \(BC\) bằng:
A. \(2,4a\)
B. \(3a\)
C. \(4a\)
D. \(5a\)
b) Khoảng cách từ điểm \(A\) đến đường thẳng \(BD\) bằng:
A. \(2,4a\)
B. \(3a\)
C. \(4a\)
D. \(5a\)
c) Khoảng cách giữa hai đường thẳng \(AB\) và \(CD\) bằng:
A. \(2,4a\)
B. \(3a\)
C. \(4a\)
D. \(5a\)
Phương pháp giải - Xem chi tiết
Khoảng cách từ 1 điểm đến 1 đường thẳng là độ dài đoạn thẳng nối điểm đó và hình chiếu của nó trên đường thẳng.
Khoảng cách giữa 2 đường thẳng song song là khoảng cách từ 1 điểm của đường thẳng này đến đường thẳng kia.
Lời giải chi tiết
a) Do \(ABCD\) là hình chữ nhật, nên ta có \(AB \bot BC\). Như vậy khoảng cách từ điểm \(A\) đến đường thẳng \(BC\) là đoạn thẳng \(AB\). Do \(AB = 3a\), nên đáp án cần chọn là đáp án B.
b) Gọi \(H\) là hình chiếu của \(A\) trên \(BD\). Khi đó khoảng cách từ \(A\) đến \(BD\) là đoạn thẳng \(AH\).
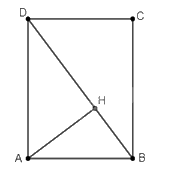
Tam giác \(ABD\) vuông tại \(A\), đường cao \(AH\) nên ta có \(BD = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} = 5a\)
Như vậy \(AH = \frac{{AB.AD}}{{BD}} = \frac{{3a.4a}}{{5a}} = 2,4a\).
Đáp án cần chọn là đáp án A.
c) Do \(AB\parallel CD\) nên khoảng cách giữa 2 đường thẳng này chính là khoảng cách từ điểm \(A\) đến đường thẳng \(CD\). Vì \(AD \bot DC\) nên khoảng cách giữa hai đường thẳng \(AB\) và \(CD\) chính là đoạn thẳng \(AD\). Mà \(AD = 4a\), nên đáp án đúng là đáp án C.
Giải bài 45 trang 109, 110 sách bài tập Toán 11 Cánh Diều: Tổng quan và hướng dẫn chi tiết
Bài 45 trang 109, 110 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng để giải quyết các bài toán thực tế.
Nội dung chính của bài 45
- Câu 1: Kiểm tra kiến thức về điều kiện song song của hai đường thẳng trong không gian.
- Câu 2: Vận dụng kiến thức về điều kiện vuông góc giữa đường thẳng và mặt phẳng.
- Câu 3: Giải quyết bài toán tìm góc giữa đường thẳng và mặt phẳng.
- Câu 4: Ứng dụng các kiến thức đã học để chứng minh các đẳng thức hình học.
Hướng dẫn giải chi tiết từng câu
Câu 1: Giải bài 45.1 trang 109 SBT Toán 11 Cánh Diều
Để giải câu 1, học sinh cần nắm vững điều kiện hai đường thẳng song song trong không gian. Cụ thể, hai đường thẳng song song khi và chỉ khi chúng không có điểm chung và các đường thẳng chứa chúng không đồng phẳng. Việc xác định các yếu tố này đòi hỏi học sinh phải hiểu rõ về vectơ chỉ phương và vectơ pháp tuyến của đường thẳng và mặt phẳng.
Ví dụ minh họa: Cho hai đường thẳng d1 và d2. Để chứng minh d1 song song với d2, ta cần chứng minh rằng vectơ chỉ phương của d1 và d2 không cùng phương và d1 không nằm trên d2.
Câu 2: Giải bài 45.2 trang 109 SBT Toán 11 Cánh Diều
Câu 2 yêu cầu học sinh vận dụng kiến thức về điều kiện vuông góc giữa đường thẳng và mặt phẳng. Một đường thẳng vuông góc với một mặt phẳng khi và chỉ khi nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. Để giải quyết bài toán này, học sinh cần xác định vectơ pháp tuyến của mặt phẳng và vectơ chỉ phương của đường thẳng.
Lưu ý: Nếu đường thẳng vuông góc với mặt phẳng, thì vectơ chỉ phương của đường thẳng sẽ cùng phương với vectơ pháp tuyến của mặt phẳng.
Câu 3: Giải bài 45.3 trang 110 SBT Toán 11 Cánh Diều
Để tìm góc giữa đường thẳng và mặt phẳng, ta sử dụng công thức: sin(α) = |cosin góc giữa vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng|. Việc tính toán cosin góc giữa hai vectơ đòi hỏi học sinh phải nắm vững kiến thức về tích vô hướng của hai vectơ.
Công thức: cos(θ) = (a1*a2 + b1*b2 + c1*c2) / (√(a1^2 + b1^2 + c1^2) * √(a2^2 + b2^2 + c2^2))
Câu 4: Giải bài 45.4 trang 110 SBT Toán 11 Cánh Diều
Câu 4 thường là bài toán chứng minh đẳng thức hình học. Để giải quyết bài toán này, học sinh cần vận dụng linh hoạt các kiến thức đã học về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng, kết hợp với các định lý và tính chất hình học đã được học.
Lời khuyên khi giải bài tập
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán và các dữ kiện đã cho.
- Vẽ hình minh họa: Hình vẽ giúp học sinh hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Vận dụng kiến thức: Sử dụng các định lý, tính chất và công thức đã học để giải quyết bài toán.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là chính xác và hợp lý.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa và sách bài tập Toán 11. Chúng tôi hy vọng rằng bài viết này sẽ giúp bạn hiểu rõ hơn về bài 45 trang 109, 110 sách bài tập Toán 11 Cánh Diều và đạt kết quả tốt trong học tập. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!