Giải bài 57 trang 118 sách bài tập toán 11 tập 2 - Cánh diều
Tổng quan nội dung
Giải bài 57 trang 118 SBT Toán 11 Tập 2 Cánh Diều
Chào mừng các em học sinh đến với lời giải chi tiết bài 57 trang 118 sách bài tập Toán 11 Tập 2 Cánh Diều. Bài viết này sẽ cung cấp đáp án chính xác và hướng dẫn giải bài tập một cách dễ hiểu nhất.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho hình chóp tứ giác đều \(S.ABCD\) có \(AB = a\), \(O\) là hình chiếu
Đề bài
Cho hình chóp tứ giác đều \(S.ABCD\) có \(AB = a\), \(O\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\), \(SO = a\). Gọi \(M\) là hình chiếu của \(O\) trên \(CD\) (xem hình dưới).
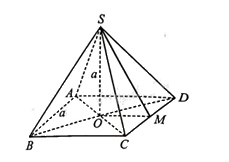
a) Đường thẳng \(AC\) vuông góc với mặt phẳng nào trong các mặt phẳng sau đây?
A. \(\left( {SAB} \right)\)
B. \(\left( {SAD} \right)\)
C. \(\left( {SBC} \right)\)
D. \(\left( {SBD} \right)\)
b) Số đo của góc nhị diện \(\left[ {A,SO,M} \right]\) bằng:
A. \({30^o}\)
B. \({45^o}\)
C. \({135^o}\)
D. \({150^o}\)
c) Khoảng cách giữa hai đường thẳng \(SO\) và \(BC\) bằng:
A. \(a\)
B. \(\frac{a}{2}\)
C. \(\frac{{a\sqrt 2 }}{2}\)
D. \(\frac{{a\sqrt 3 }}{2}\)
d) Thể tích của khối chóp \(S.ABCD\) bằng:
A. \({a^3}\)
B. \(\frac{{{a^3}}}{2}\)
C. \(\frac{{{a^3}}}{3}\)
D. \(3{a^3}\)
e) Khoảng cách từ \(C\) đến mặt phẳng \(\left( {SOM} \right)\) bằng:
A. \(a\)
B. \(\frac{a}{2}\)
C. \(\frac{{a\sqrt 2 }}{2}\)
D. \(\frac{{a\sqrt 3 }}{2}\)
g) Côtang của góc giữa đường thẳng \(SM\) và \(\left( {ABCD} \right)\) bằng:
A. \(\frac{1}{2}\)
B. \(2\)
C. \(1\)
D. \(\frac{{\sqrt 5 }}{5}\)
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về đường thẳng vuông góc với mặt phẳng
b) Xác định góc phẳng nhị diện của góc nhị diện \(\left[ {A,SO,M} \right]\).
c) Xác định đường vuông góc chung của hai đường thẳng \(SO\) và \(BC\).
d) Công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\), với \(S\) là diện tích đáy và \(h\) là chiều cao của khối chóp đó.
e) Chứng minh rằng \(M\) là hình chiếu của \(C\) trên \(\left( {SOM} \right)\), từ đó khoảng cách cần tính là đoạn thẳng \(CM\).
g) Xác định góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABCD} \right)\), rồi tính côtang của góc đó.
Lời giải chi tiết
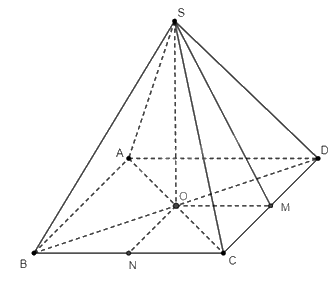
a) Do \(S.ABCD\) là hình chóp tứ giác đều, ta suy ra \(ABCD\) là hình vuông. Điều này suy ra \(AC \bot BD\).
Hơn nữa, do \(SO \bot \left( {ABCD} \right)\) nên \(SO \bot AC\).
Như vậy, do \(AC \bot BD\), \(SO \bot AC\) nên \(AC \bot \left( {SBD} \right)\)
Đáp án đúng là D.
b) Do \(SO \bot \left( {ABCD} \right)\), ta suy ra \(SO \bot AO\) và \(SO \bot OM\). Do đó, góc \(\widehat {AOM}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,SO,M} \right]\).
Do \(M\) là trung điểm của \(CD\), và tam giác \(COD\) vuông cân tại \(O\), ta suy ra \(\widehat {MOD} = {45^o}\) và \(OM \bot CD\). Do đó \(\widehat {AOM} = \widehat {AOD} + \widehat {MOD} = {90^o} + {45^o} = {135^o}\).
Vậy số đo của góc nhị diện \(\left[ {A,SO,M} \right]\) là \({135^o}\).
Đáp án đúng là C.
c) Gọi \(N\) là trung điểm của \(BC\). Tam giác \(OBC\) vuông cân tại \(O\), nên ta có \(ON \bot BC\). Hơn nữa, do \(SO \bot \left( {ABCD} \right)\), nên \(SO \bot ON\).
Vậy \(ON\) là đường vuông góc chung của \(SO\) và \(BC\), do đó khoảng cách giữa hai đường thẳng \(SO\) và \(BC\) là đoạn thẳng \(ON\).
Dễ dàng chứng minh được \(ON = \frac{1}{2}AB = \frac{a}{2}\), vậy khoảng cách giữa hai đường thẳng chéo nhau \(SO\) và \(BC\) bằng \(\frac{a}{2}\).
Đáp án đúng là B.
d) Thể tích khối chóp \(S.ABCD\) là \(V = \frac{1}{3}Sh = \frac{1}{3}A{B^2}.SO = \frac{1}{3}{a^2}.a = \frac{{{a^3}}}{3}\).
Đáp án đúng là C.
e) Do \(SO \bot \left( {ABCD} \right)\), ta suy ra \(SO \bot CM\), mà theo câu b, ta suy ra \(CM \bot OM\).
Từ đó ta có \(CM \bot \left( {SOM} \right)\). Như vậy \(M\) là hình chiếu của \(C\) trên \(\left( {SOM} \right)\), từ đó khoảng cách từ \(C\) đến \(\left( {SOM} \right)\) là đoạn thẳng \(CM\). Do \(CM = \frac{1}{2}CD = \frac{a}{2}\), nên khoảng cách từ \(C\) đến \(\left( {SOM} \right)\) bằng \(\frac{a}{2}\).
Đáp án đúng là B.
g) Do \(O\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\), ta suy ra góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABCD} \right)\) là góc \(\widehat {SMO}\).
Ta có \(\cot \widehat {SMO} = \frac{{OM}}{{SO}} = \frac{{\frac{a}{2}}}{a} = \frac{1}{2}\).
Vậy côtang của góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(\frac{1}{2}\).
Đáp án đúng là A.
Giải bài 57 trang 118 SBT Toán 11 Tập 2 Cánh Diều: Tổng quan và Phương pháp giải
Bài 57 trang 118 sách bài tập Toán 11 Tập 2 Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp để giải quyết các bài toán thực tế.
Nội dung bài 57 trang 118 SBT Toán 11 Tập 2 Cánh Diều
Bài 57 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của một hàm số cho trước, có thể là hàm số đơn giản hoặc hàm số phức tạp.
- Tìm đạo hàm tại một điểm: Yêu cầu tìm giá trị đạo hàm của hàm số tại một điểm cụ thể.
- Ứng dụng đạo hàm để giải quyết các bài toán liên quan đến vận tốc, gia tốc: Đây là dạng bài tập ứng dụng thực tế, yêu cầu học sinh hiểu rõ ý nghĩa của đạo hàm trong vật lý.
- Khảo sát hàm số: Sử dụng đạo hàm để xác định khoảng đồng biến, nghịch biến, cực trị của hàm số.
Hướng dẫn giải chi tiết bài 57 trang 118 SBT Toán 11 Tập 2 Cánh Diều
Để giải quyết bài 57 trang 118 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Các công thức đạo hàm cơ bản: Đạo hàm của xn, sinx, cosx, tanx, cotx, ex, ln(x),...
- Các quy tắc tính đạo hàm: Quy tắc cộng, trừ, nhân, chia, quy tắc hàm hợp.
- Ý nghĩa hình học của đạo hàm: Hệ số góc của tiếp tuyến tại một điểm.
Ví dụ minh họa:
Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1. Ta sẽ áp dụng quy tắc đạo hàm của tổng và các công thức đạo hàm cơ bản để giải:
f'(x) = 3x2 + 4x - 5
Lưu ý khi giải bài tập
- Đọc kỹ đề bài để xác định đúng yêu cầu của bài toán.
- Sử dụng các công thức đạo hàm một cách chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
- Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.
Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín
Tusach.vn cung cấp đầy đủ lời giải chi tiết các bài tập trong sách bài tập Toán 11 Tập 2 Cánh Diều, cùng với các tài liệu học tập hữu ích khác như lý thuyết, bài tập trắc nghiệm, đề thi thử,...
Chúng tôi luôn cập nhật nội dung mới nhất và đảm bảo tính chính xác của thông tin. Hãy truy cập tusach.vn để đồng hành cùng chúng tôi trên con đường chinh phục môn Toán!
Bảng tổng hợp các công thức đạo hàm thường dùng
| Hàm số | Đạo hàm |
|---|---|
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sinx | f'(x) = cosx |
| f(x) = cosx | f'(x) = -sinx |