Giải bài 62 trang 31 SBT Toán 11 Cánh Diều

Giải bài 62 trang 31 sách bài tập toán 11 - Cánh diều

Tusach.vn xin giới thiệu lời giải chi tiết bài 62 trang 31 sách bài tập Toán 11 Cánh Diều. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cố gắng cung cấp những nội dung chất lượng, chính xác và cập nhật nhất để hỗ trợ học sinh trong quá trình học tập.

Mực nước cao nhất tại một cảng biển là 16 m khi thuỷ triều lên cao và sau 12 giờ khi thuỷ triều xuống thấp thì mực nước thấp nhất là 10 m.

Đề bài

Mực nước cao nhất tại một cảng biển là 16 m khi thuỷ triều lên cao và sau 12 giờ khi thuỷ triều xuống thấp thì mực nước thấp nhất là 10 m. Đồ thị ở hình bên mô tả sự thay đổi chiều cao của mực nước tại cảng trong vòng 24 giờ tính từ lúc nửa đêm. Biết chiều cao của mực nước \(h\) (m) theo thời gian \(t\)(h) \(\left( {0 \le t \le 24} \right)\) được cho bởi công thức \(h = m + a\cos \left( {\frac{\pi }{{12}}t} \right)\) với \(m\), \(a\) là các số thực dương cho trước.

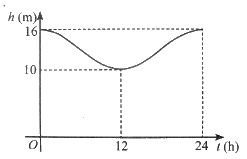
Giải bài 62 trang 31 sách bài tập toán 11 - Cánh diều 1

a) Tìm \(m\), \(a\).

b) Tìm thời điểm trong ngày khi chiều cao của mực nước là 11,5 m.

Phương pháp giải - Xem chi tiết Giải bài 62 trang 31 sách bài tập toán 11 - Cánh diều 2

a) Mực nước thấp nhất đạt được là \(m - a\) khi \(\cos \left( {\frac{\pi }{{12}}t} \right) = - 1\)

Mực nước cao nhất đạt được là \(m + a\) khi \(\cos \left( {\frac{\pi }{{12}}t} \right) = 1\)

Từ đó tìm được \(m\) và \(a\).

b) Với \(m\) và \(a\) tìm được ở câu a, để tìm thời điểm trong ngày khi chiều cao của mực nước là 11,5 m, ta sẽ giải phương trình ẩn \(t\): \(h = 11,5\) và kết luận.

Lời giải chi tiết

a) Do \( - 1 \le \cos \left( {\frac{\pi }{{12}}t} \right) \le 1 \Rightarrow m - a \le h \le m + a\).

Mực nước thấp nhất đạt được là \(m - a\) (m), mực nước cao nhất đạt được là \(m + a\) (m).

Theo đề bài, ta có hệ phương trình: \(\left\{ \begin{array}{l}m - a = 10\\m + a = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 13\\a = 3\end{array} \right.\)

\( \Rightarrow h = 13 + 3\cos \left( {\frac{\pi }{{12}}t} \right)\)

b) Để tìm thời điểm trong ngày khi chiều cao của mực nước là 11,5 m, ta sẽ giải phương trình: \(h = 11,5 \Leftrightarrow 13 + 3\cos \left( {\frac{\pi }{{12}}t} \right) = 11,5 \Leftrightarrow \cos \left( {\frac{\pi }{{12}}t} \right) = \frac{{ - 1}}{2}\)

\( \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{{12}}t = \frac{{2\pi }}{3} + k2\pi \\\frac{\pi }{{12}}t = - \frac{{2\pi }}{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 8 + 24k\\t = - 8 + 24k\end{array} \right.\)\(\left( {k \in \mathbb{Z}} \right)\)

Như vậy, tại thời điểm \(t = 8\)(h) và \(t = 16\)(h), chiều cao của mực nước là 11,5 m.

Giải bài 62 trang 31 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải

Bài 62 trang 31 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về vectơ, các phép toán vectơ, và ứng dụng của vectơ trong hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các công thức liên quan.

Nội dung bài 62 trang 31 SBT Toán 11 Cánh Diều

Bài 62 thường yêu cầu học sinh thực hiện các thao tác sau:

Tìm tọa độ của một vectơ.
Thực hiện các phép toán vectơ (cộng, trừ, nhân với một số).
Chứng minh các đẳng thức vectơ.
Ứng dụng vectơ để giải các bài toán hình học (ví dụ: chứng minh ba điểm thẳng hàng, hai đường thẳng song song, vuông góc).

Phương pháp giải bài 62 trang 31 SBT Toán 11 Cánh Diều

Xác định rõ yêu cầu của bài toán: Đọc kỹ đề bài để hiểu rõ những gì cần tìm hoặc chứng minh.
Sử dụng các công thức và định lý liên quan: Áp dụng các công thức về tọa độ vectơ, các phép toán vectơ, và các định lý hình học để giải quyết bài toán.
Biểu diễn các vectơ bằng tọa độ: Nếu bài toán liên quan đến hình học, hãy biểu diễn các vectơ bằng tọa độ để dễ dàng thực hiện các phép toán.
Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Lời giải chi tiết bài 62 trang 31 SBT Toán 11 Cánh Diều

(Giả sử bài 62 có nội dung cụ thể là: Cho A(1;2), B(3;4), C(5;6). Tìm tọa độ của vectơ AB và tính độ dài của vectơ AB.)

Lời giải:

Vectơ AB có tọa độ là: AB = (3-1; 4-2) = (2; 2)

Độ dài của vectơ AB là: |AB| = √((2)^2 + (2)^2) = √(4+4) = √8 = 2√2

Các bài tập tương tự và luyện tập

Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, học sinh có thể tham khảo các bài tập tương tự trong sách bài tập Toán 11 Cánh Diều và các tài liệu tham khảo khác. Ngoài ra, việc luyện tập thường xuyên cũng rất quan trọng để nắm vững kiến thức và tự tin giải các bài toán khó hơn.

Ví dụ bài tập luyện tập

Cho A(0;1), B(2;3), C(4;5). Tìm tọa độ của vectơ AC và so sánh vectơ AB và AC.

Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín

Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập Toán 11, bao gồm sách giáo khoa, sách bài tập, đề thi, và lời giải chi tiết. Chúng tôi cam kết cung cấp những nội dung chất lượng, chính xác và cập nhật nhất để hỗ trợ học sinh trong quá trình học tập. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!

Chủ đề	Liên kết
Giải bài tập Toán 11 Cánh Diều	https://tusach.vn/toan-11-canh-dieu
Sách bài tập Toán 11 Cánh Diều	https://tusach.vn/sbt-toan-11-canh-dieu