Giải bài 42 trang 104 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 42 trang 104 SBT Toán 11 Cánh Diều
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 42 trang 104 sách bài tập Toán 11 Cánh Diều. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất.
Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng cần thiết để tự tin giải quyết các bài toán tương tự.
Cho hình chóp \(S.ABC\) có \(\widehat {ASB} = \widehat {ASC} = {90^o}\).
Đề bài
Cho hình chóp \(S.ABC\) có \(\widehat {ASB} = \widehat {ASC} = {90^o}\). Gọi \(H\) là trực tâm của tam giác \(ABC\). Chứng minh rằng \(\left( {SAH} \right) \bot \left( {ABC} \right)\).
Phương pháp giải - Xem chi tiết
Để chứng minh 2 mặt phẳng vuông góc, ta cần chứng minh 1 đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia.
Lời giải chi tiết
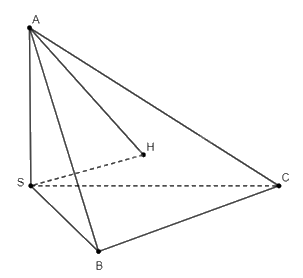
Do \(H\) là trực tâm của tam giác \(ABC\) nên ta có \(AH \bot BC\).
Do \(\widehat {ASB} = \widehat {ASC} = {90^o}\) nên ta suy ra \(SA \bot SB\) và \(SA \bot SC\). Suy ra \(SA \bot \left( {BSC} \right)\), từ đó \(SA \bot BC\).
Như vậy, vì \(AH \bot BC\), \(SA \bot BC\) nên \(\left( {SAH} \right) \bot BC\).
Mà \(BC \subset \left( {ABC} \right)\), nên \(\left( {SAH} \right) \bot \left( {ABC} \right)\). Bài toán được chứng minh.
Giải bài 42 trang 104 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải
Bài 42 trang 104 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về Đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit và các phép toán trên hàm số (tổng, hiệu, tích, thương, hàm hợp).
Nội dung chi tiết bài 42 trang 104 SBT Toán 11 Cánh Diều
Để giải quyết bài 42 trang 104 SBT Toán 11 Cánh Diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Quy tắc tính đạo hàm của hàm số cơ bản: Đạo hàm của xn, sin(x), cos(x), ex, ln(x),...
- Quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
- Quy tắc đạo hàm của hàm hợp: u'(x) * f'(u(x))
- Các công thức đạo hàm đặc biệt: Ví dụ, đạo hàm của tan(x), cot(x),...
Hướng dẫn giải chi tiết bài 42 trang 104 SBT Toán 11 Cánh Diều
Dưới đây là hướng dẫn giải chi tiết cho từng phần của bài 42 trang 104 SBT Toán 11 Cánh Diều. (Lưu ý: Nội dung cụ thể của bài tập sẽ được trình bày chi tiết tại đây, ví dụ:)
Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1
Giải:
f'(x) = d/dx (3x2) + d/dx (2x) - d/dx (1)
f'(x) = 6x + 2 - 0
f'(x) = 6x + 2
Ví dụ 2: Tính đạo hàm của hàm số g(x) = sin(x) * cos(x)
Giải:
g'(x) = d/dx (sin(x)) * cos(x) + sin(x) * d/dx (cos(x))
g'(x) = cos(x) * cos(x) + sin(x) * (-sin(x))
g'(x) = cos2(x) - sin2(x)
Mẹo giải nhanh bài tập đạo hàm
Để giải nhanh các bài tập về đạo hàm, bạn có thể áp dụng một số mẹo sau:
- Nắm vững các công thức đạo hàm cơ bản: Điều này giúp bạn tiết kiệm thời gian và tránh sai sót.
- Sử dụng quy tắc đạo hàm một cách linh hoạt: Đặc biệt là quy tắc đạo hàm của hàm hợp.
- Biến đổi biểu thức trước khi tính đạo hàm: Đôi khi, việc biến đổi biểu thức có thể giúp bạn đơn giản hóa bài toán.
- Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập tương tự và luyện tập
Để củng cố kiến thức và kỹ năng, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 11 Cánh Diều và các tài liệu tham khảo khác. tusach.vn sẽ tiếp tục cập nhật thêm nhiều lời giải chi tiết cho các bài tập khác trong chương trình học.
Kết luận
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 42 trang 104 SBT Toán 11 Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!