Giải bài 47 trang 23 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 47 trang 23 SBT Toán 11 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 47 trang 23 sách bài tập Toán 11 Cánh Diều. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập.
Chúng tôi luôn cố gắng cung cấp những nội dung chất lượng, chính xác và cập nhật nhất để hỗ trợ học sinh trong quá trình học tập.
Một vòng quay trò chơi có bán kinh 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút
Đề bài
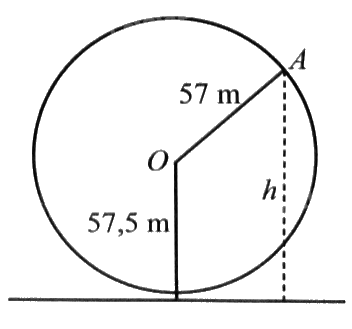
Một vòng quay trò chơi có bán kinh 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách \(h\) (m) từ một cabin gắn tại điểm \(A\) của vòng quay đến mặt đất được tính bởi công thức \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\); với \(t\) là thời gian quay của vòng quay tính bằng phút \(\left( {t \ge 0} \right)\) (Xem hình vẽ)
a) Tính chu kì của hàm số \(h\left( t \right)\)
b) Khi \(t = 0\) (phút) thì khoảng cách của cabin đến mặt đất bằng bao nhiêu?
c) Khi quay một vòng lần thứ nhất tính từ thời điểm \(t = 0\) (phút), tại thời điểm nào của \(t\) thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao 86 m?
Phương pháp giải - Xem chi tiết
a) Chu kì của hàm số chính là thời gian bán kính vòng quay quay hết 1 vòng.
b) Thay \(t = 0\) vào hàm số \(h\left( t \right)\) để tính khoảng cách của cabin đến mặt đất.
c) Cabin ở vị trí cao nhất khi hàm số \(h\left( t \right)\) đạt giá trị lớn nhất. Sử dụng tính chất \( - 1 \le \sin x \le 1\) để tìm giá trị lớn nhất của hàm \(h\left( t \right)\).
Lời giải chi tiết
a) Chu kì của hàm số chính là thời gian bán kính vòng quay quay hết 1 vòng. Do vòng quay trò chơi quay mỗi vòng hết 15 phút, chu kì của hàm số này là 15 phút.
b) Khoảng cách của cabin đến mặt đất tại thời điểm \(t = 0\) (phút) là:
\(h\left( 0 \right) = 57\sin \left( { - \frac{\pi }{2}} \right) + 57,5 = 0,5\) (m)
c) Do \(\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) \le 1 \Rightarrow 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) \le 57 \Rightarrow h\left( t \right) \le 114,5\)
Dấu bằng xảy ra \( \Leftrightarrow \sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) = 1 \Leftrightarrow \frac{{2\pi }}{{15}}t - \frac{\pi }{2} = \frac{\pi }{2} + k2\pi \Leftrightarrow \frac{{2\pi }}{{15}}t = \pi + k2\pi \)
\( \Leftrightarrow t = \frac{{15}}{2} + 15k\) \(\left( {k \in \mathbb{Z}} \right)\)
Như vậy, kể từ thời điểm \(t = 0\) (phút), cabin đạt vị trí cao nhất tại thời điểm \(t = 7,5\) (phút)
Để tìm thời gian cabin đạt độ cao 86 m, ta cần phải tìm các giá trị của \(t\) để \(h\left( t \right) = 86\).
Ta có \(h\left( t \right) = 86 \Rightarrow 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5 = 86 \Rightarrow \sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) = \frac{1}{2}\)
Theo Bài 46, ta có \(\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}\frac{{2\pi }}{{15}}t - \frac{\pi }{2} = \frac{\pi }{6} + k2\pi \\\frac{{2\pi }}{{15}}t - \frac{\pi }{2} = \frac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 5 + 15k\\t = 10 + 15k\end{array} \right.\)
Như vậy, kể từ thời điểm \(t = 0\) (phút), cabin đạt được chiều cao 86 m lần đầu tiên khi \(t = 5\) (phút)
Giải bài 47 trang 23 SBT Toán 11 Cánh Diều: Tổng quan
Bài 47 trang 23 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về vectơ, các phép toán vectơ, và ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh phải hiểu rõ định nghĩa, tính chất của vectơ, cũng như các công thức liên quan để giải quyết một cách chính xác.
Nội dung chi tiết bài 47 trang 23 SBT Toán 11 Cánh Diều
Để giúp các em học sinh hiểu rõ hơn về bài tập này, Tusach.vn sẽ trình bày chi tiết nội dung bài tập và lời giải:
Phần 1: Đề bài
(Nội dung đề bài bài 47 trang 23 SBT Toán 11 Cánh Diều sẽ được chèn vào đây. Ví dụ:)
Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo vectơ AB và AC.
Phần 2: Lời giải chi tiết
Lời giải:
Ta có: AM = (AB + AC) / 2
(Giải thích chi tiết từng bước giải, kèm theo hình vẽ minh họa nếu cần thiết)
Phần 3: Phương pháp giải và lưu ý
Để giải bài tập này, các em cần nắm vững:
- Định nghĩa vectơ.
- Các phép toán vectơ (cộng, trừ, nhân với một số).
- Quy tắc trung điểm.
- Cách biểu diễn một vectơ qua các vectơ khác.
Lưu ý:
- Khi giải bài tập về vectơ, hãy vẽ hình để dễ hình dung và tìm ra mối liên hệ giữa các vectơ.
- Sử dụng các quy tắc và công thức vectơ một cách chính xác.
- Kiểm tra lại kết quả để đảm bảo tính đúng đắn.
Các bài tập tương tự
Để củng cố kiến thức, các em có thể tham khảo thêm các bài tập tương tự sau:
- Bài 48 trang 23 SBT Toán 11 Cánh Diều
- Bài 49 trang 24 SBT Toán 11 Cánh Diều
- ...
Tusach.vn – Đồng hành cùng học sinh
Tusach.vn là website chuyên cung cấp lời giải bài tập Toán, Lý, Hóa, Sinh, Anh, Văn lớp 6, 7, 8, 9, 10, 11, 12. Chúng tôi luôn cập nhật những lời giải mới nhất, chính xác nhất và dễ hiểu nhất để giúp các em học sinh học tập tốt hơn. Hãy truy cập Tusach.vn để được hỗ trợ!
| Chương | Bài | Link |
|---|---|---|
| Chương 1 | Bài 47 | https://tusach.vn/giai-bai-47-trang-23-sbt-toan-11-canh-dieu |
| Chương 1 | Bài 48 | https://tusach.vn/giai-bai-48-trang-23-sbt-toan-11-canh-dieu |