Giải bài 20 trang 95 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 20 trang 95 SBT Toán 11 Cánh Diều
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 20 trang 95 sách bài tập Toán 11 Cánh Diều. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi đã biên soạn hướng dẫn này để giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Bài viết này sẽ cung cấp đáp án, phương pháp giải và những lưu ý quan trọng để bạn có thể hoàn thành bài tập một cách hiệu quả nhất.
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right).\) Gọi M, N, P lần lượt là trọng tâm của ba tam giác SAB, SBC, SCA
Đề bài
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right).\) Gọi M, N, P lần lượt là trọng tâm của ba tam giác SAB, SBC, SCA. Chứng minh rằng \(SA \bot \left( {MNP} \right).\)
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Lời giải chi tiết
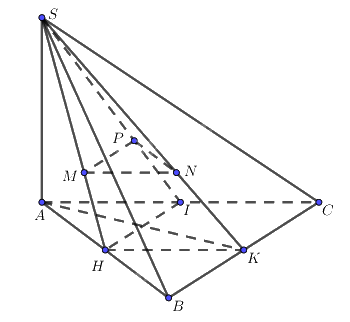
Gọi H, K, I lần lượt là trung điểm của AB, BC, CA.
Theo giả thiết ta có: \(\frac{{SM}}{{SH}} = \frac{{SN}}{{SK}} = \frac{{SP}}{{SI}} = \frac{2}{3}.\)
Theo định lý Ta-lét: Trong tam giác SHK có \(MN{\rm{ // }}HK,\) trong tam giác SHI có \(MP{\rm{ // }}HI.\) Mà \(HK \subset \left( {ABC} \right),{\rm{ }}HI \subset \left( {ABC} \right)\) nên \(MN{\rm{ // }}\left( {ABC} \right),{\rm{ }}MP{\rm{ // }}\left( {ABC} \right).\)Mà, MN, MP cắt nhau trong mặt phẳng (MNP) nên \(\left( {MNP} \right){\rm{ // }}\left( {ABC} \right).\)
Ta lại có, \(SA \bot \left( {ABC} \right).\) Vậy \(SA \bot \left( {MNP} \right).\)
Giải bài 20 trang 95 SBT Toán 11 Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Bài 20 trang 95 sách bài tập Toán 11 Cánh Diều thuộc chương trình học môn Toán lớp 11, tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng để giải quyết các bài toán thực tế.
Nội dung chính của bài 20 trang 95 SBT Toán 11 Cánh Diều
Bài tập 20 thường bao gồm các dạng bài sau:
- Xác định mối quan hệ giữa đường thẳng và mặt phẳng: Kiểm tra xem một đường thẳng có song song, vuông góc hay cắt một mặt phẳng hay không.
- Chứng minh tính song song, vuông góc: Sử dụng các định lý, tính chất để chứng minh mối quan hệ giữa đường thẳng và mặt phẳng.
- Tính góc giữa đường thẳng và mặt phẳng: Áp dụng công thức tính góc để tìm góc cần tìm.
- Tìm giao điểm, giao tuyến: Xác định giao điểm của đường thẳng và mặt phẳng, giao tuyến của hai mặt phẳng.
Hướng dẫn giải chi tiết từng phần của bài 20
Để giúp bạn hiểu rõ hơn về cách giải bài 20 trang 95 SBT Toán 11 Cánh Diều, chúng tôi sẽ trình bày chi tiết lời giải cho từng phần của bài tập:
Câu a: ... (Giải thích chi tiết câu a với các bước giải cụ thể)
Ví dụ:
- Bước 1: Xác định các yếu tố liên quan đến bài toán (đường thẳng, mặt phẳng, điểm...).
- Bước 2: Áp dụng định lý, tính chất phù hợp để chứng minh hoặc tính toán.
- Bước 3: Kết luận.
Câu b: ... (Giải thích chi tiết câu b với các bước giải cụ thể)
Câu c: ... (Giải thích chi tiết câu c với các bước giải cụ thể)
Lưu ý quan trọng khi giải bài 20 trang 95 SBT Toán 11 Cánh Diều
Để đạt kết quả tốt nhất khi giải bài tập này, bạn cần lưu ý những điều sau:
- Nắm vững kiến thức lý thuyết: Hiểu rõ các định lý, tính chất về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng.
- Vẽ hình minh họa: Vẽ hình giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Sử dụng các công cụ hỗ trợ: Sử dụng thước, compa, máy tính để vẽ hình và tính toán chính xác.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Ví dụ minh họa thêm
Để giúp bạn hiểu sâu hơn về cách giải các bài toán liên quan đến đường thẳng và mặt phẳng, chúng ta cùng xem xét một ví dụ minh họa sau:
Bài toán: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng AM song song với mặt phẳng (SCD).
Lời giải:
- Gọi N là trung điểm của cạnh CD.
- Chứng minh rằng MN song song với SD.
- Chứng minh rằng MN nằm trong mặt phẳng (SCD).
- Từ đó suy ra AM song song với mặt phẳng (SCD).
Tổng kết
Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 20 trang 95 sách bài tập Toán 11 Cánh Diều. Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi tại tusach.vn để được hỗ trợ.
Chúc bạn học tập tốt!