Giải bài 47 trang 110 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 47 trang 110 SBT Toán 11 Cánh Diều
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 47 trang 110 sách bài tập Toán 11 Cánh Diều. Bài viết này sẽ giúp bạn hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu và phù hợp với chương trình học Toán 11 hiện hành.
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), \(AB \bot BC\), \(SA = AB = 3a\), \(BC = 4a\). Tính khoảng cách:
Đề bài
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), \(AB \bot BC\), \(SA = AB = 3a\), \(BC = 4a\). Tính khoảng cách:
a) Từ điểm \(C\) đến mặt phẳng \(\left( {SAB} \right)\).
b) Giữa hai đường thẳng \(SA\) và \(BC\).
c) Từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\).
d) Từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
e*) Giữa hai đường thẳng \(AB\) và \(SC\).
Phương pháp giải - Xem chi tiết
a) Chỉ ra rằng \(B\) là hình chiếu của \(C\) trên \(\left( {SAB} \right)\), từ đó tính được khoảng cách từ \(C\) đến mặt phẳng \(\left( {SAB} \right)\).
b) Chỉ ra rằng \(AB\) là đường vuông góc chung của hai đường thẳng \(SA\) và \(BC\), từ đó tính được khoảng cách giữa hai đường thẳng \(SA\) và \(BC\).
c) Gọi \(H\) là hình chiếu của điểm \(A\) trên \(SB\). Ta chứng minh \(H\) cũng là hình chiếu của điểm \(A\) trên mặt phẳng \(\left( {SBC} \right)\), từ đó khoảng cách cần tính là đoạn thẳng \(AH\).
d) Gọi \(M\) là hình chiếu của điểm \(B\) trên \(AC\). Ta chứng minh \(M\) cũng là hình chiếu của điểm \(B\) trên mặt phẳng \(\left( {SAC} \right)\), từ đó khoảng cách cần tính là đoạn thẳng \(BM\).
e) Lấy điểm \(D \in \left( {ABC} \right)\) sao cho \(ABCD\) là hình bình hành. Gọi \(N\) là hình chiếu của \(A\) trên \(SD\). Ta chứng minh \(AN \bot \left( {SCD} \right)\). Do \(AB\parallel CD\) nên \(AB\parallel \left( {SCD} \right)\). Mà \(SC \in \left( {SCD} \right)\) nên khoảng cách giữa \(AB\) và \(SC\) chính là khoảng cách giữa \(AB\) và \(\left( {SCD} \right)\)
Lời giải chi tiết
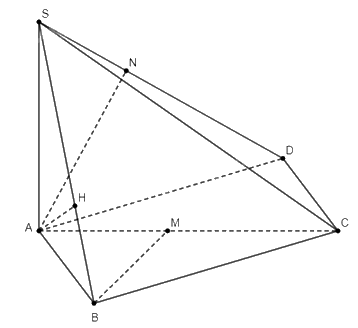
a) Do \(SA \bot \left( {ABC} \right)\), ta có \(SA \bot BC\). Mà \(AB \bot BC\) nên \(\left( {SAB} \right) \bot BC\). Do đó, \(B\) là hình chiếu của \(C\) trên \(\left( {SAB} \right)\), tức là khoảng cách từ \(C\) đến \(\left( {SAB} \right)\) là đoạn thẳng \(BC\). Do \(BC = 4a\), nên khoảng cách từ \(C\) đến \(\left( {SAB} \right)\) là \(4a\).
b) Do \(SA \bot \left( {ABC} \right)\), ta có \(SA \bot AB\). Mà \(AB \bot BC\) nên \(AB\) là đường vuông góc chung của hai đường thẳng \(SA\) và \(BC\). Suy ra khoảng cách giữa hai đường thẳng \(SA\) và \(BC\) là đoạn thẳng \(AB\). Do \(AB = 3a\), nên khoảng cách giữa hai đường thẳng \(SA\) và \(BC\) là \(3a\).
c) Gọi \(H\) là hình chiếu của điểm \(A\) trên \(SB\). Theo câu a, ta có \(\left( {SAB} \right) \bot BC\) nên \(AH \bot BC\). Vì \(AH \bot BC\), \(AH \bot SB\), ta có \(AH \bot \left( {SBC} \right)\). Vậy \(H\) là hình chiếu của điểm \(A\) trên mặt phẳng \(\left( {SBC} \right)\), điều này có nghĩa khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) là đoạn thẳng \(AH\).
Tam giác \(SAB\) vuông cân tại \(A\), \(SA = AB = 3a\) nên ta suy ra \(AH = \frac{{3a\sqrt 2 }}{2}\).
d) Gọi \(M\) là hình chiếu của điểm \(B\) trên \(AC\). Do \(SA \bot \left( {ABC} \right)\), ta suy ra \(SA \bot BM\). Vì \(SA \bot BM\), \(AC \bot BM\) nên \(\left( {SAC} \right) \bot BM\). Vậy \(M\) là hình chiếu của điểm \(B\) trên mặt phẳng \(\left( {SAC} \right)\), điều này có nghĩa khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\) là đoạn thẳng \(BM\).
Tam giác \(ABC\) vuông tại \(B\), đường cao \(BM\), nên ta có \(\frac{1}{{B{M^2}}} = \frac{1}{{B{A^2}}} + \frac{1}{{B{C^2}}}\).
Suy ra \(BM = \frac{{BA.BC}}{{\sqrt {B{A^2} + B{C^2}} }} = \frac{{3a.4a}}{{\sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} }} = \frac{{12a}}{5}\).
e) Lấy điểm \(D \in \left( {ABC} \right)\) sao cho \(ABCD\) là hình bình hành. Do \(\widehat {ABC} = {90^o}\) nên \(ABCD\) là hình chữ nhật. Suy ra \(CD \bot AD\). Do \(SA \bot \left( {ABC} \right)\), ta có \(SA \bot CD\). Do đó \(CD \bot \left( {SAD} \right)\).
Gọi \(N\) là hình chiếu của điểm \(A\) trên \(SD\). Do \(CD \bot \left( {SAD} \right)\) nên \(CD \bot AN\).
Như vậy ta có \(CD \bot AN\), \(AN \bot SD\) nên \(AN \bot \left( {SCD} \right)\). Do \(AB\parallel CD\) nên \(AB\parallel \left( {SCD} \right)\). Mà \(SC \in \left( {SCD} \right)\) nên khoảng cách giữa \(AB\) và \(SC\) chính là khoảng cách giữa \(AB\) và \(\left( {SCD} \right)\), và nó cũng chính bằng khoảng cách từ điểm \(A\) đến \(\left( {SCD} \right)\), và bằng \(AN\).
Tam giác \(SAD\) vuông tại \(A\), ta có
\(AN = \frac{{SA.AD}}{{SD}} = \frac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{{3a.4a}}{{\sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} }} = \frac{{12a}}{5}\)
Giải bài 47 trang 110 SBT Toán 11 Cánh Diều: Tổng quan
Bài 47 trang 110 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về Đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit và các phép toán trên hàm số (tổng, hiệu, tích, thương, hàm hợp).
Nội dung chi tiết bài 47 trang 110 SBT Toán 11 Cánh Diều
Để giải quyết bài 47 trang 110 SBT Toán 11 Cánh Diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Quy tắc tính đạo hàm của hàm số cơ bản: Đạo hàm của xn, sin(x), cos(x), ex, ln(x),...
- Quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
- Quy tắc đạo hàm của hàm hợp: u'(x) * f'(u(x))
Hướng dẫn giải chi tiết bài 47 trang 110 SBT Toán 11 Cánh Diều
Dưới đây là hướng dẫn giải chi tiết cho từng câu hỏi trong bài 47 trang 110 SBT Toán 11 Cánh Diều. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, dễ hiểu để bạn có thể theo dõi và tự học.
Ví dụ minh họa (Giả định một câu hỏi cụ thể trong bài 47):
Câu hỏi: Tính đạo hàm của hàm số f(x) = 2x3 - 5x2 + 7x - 1.
Giải:
- Áp dụng quy tắc đạo hàm của hàm đa thức: (xn)' = nxn-1
- f'(x) = 2 * 3x2 - 5 * 2x + 7
- f'(x) = 6x2 - 10x + 7
Kết luận: Đạo hàm của hàm số f(x) = 2x3 - 5x2 + 7x - 1 là f'(x) = 6x2 - 10x + 7.
Mẹo giải nhanh bài tập đạo hàm
Để giải nhanh các bài tập về đạo hàm, bạn có thể áp dụng một số mẹo sau:
- Nắm vững các công thức đạo hàm cơ bản.
- Phân tích cấu trúc của hàm số để chọn quy tắc đạo hàm phù hợp.
- Thực hành thường xuyên để làm quen với các dạng bài tập khác nhau.
Luyện tập thêm
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 11 Cánh Diều hoặc trên các trang web học toán trực tuyến.
Kết luận
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ cách giải bài 47 trang 110 SBT Toán 11 Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!
Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại để lại bình luận bên dưới. Chúng tôi sẽ cố gắng trả lời bạn trong thời gian sớm nhất.
| Công thức | Mô tả |
|---|---|
| (xn)' | Đạo hàm của x mũ n |
| (sin(x))' | Đạo hàm của sin x |