Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 19 trang 76 sách bài tập toán 11 - Cánh diều
SBT Toán 11 - Cánh diều
SBT TOÁN TẬP 1 - CÁNH DIỀU
Chương III. Giới hạn. Hàm số liên tục
Bài 2. Giới hạn của hàm số

Giải bài 19 trang 76 sách bài tập toán 11 - Cánh diều

Giải bài 19 trang 76 SBT Toán 11 Cánh Diều

Tusach.vn xin giới thiệu lời giải chi tiết bài 19 trang 76 sách bài tập Toán 11 Cánh Diều. Bài tập này thuộc chương trình học Toán 11, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Chúng tôi cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu sắc kiến thức và tự tin làm bài tập.

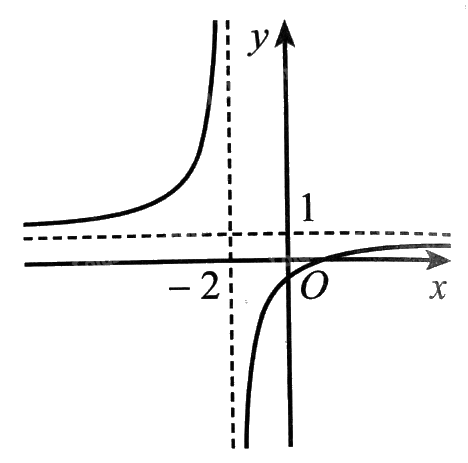
Quan sát đồ thị hàm số ở hình dưới đây và cho biết các giới hạn sau

Đề bài

Quan sát đồ thị hàm số ở hình dưới đây và cho biết các giới hạn sau: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right)\).

Giải bài 19 trang 76 sách bài tập toán 11 - Cánh diều 1

Phương pháp giải - Xem chi tiếtGiải bài 19 trang 76 sách bài tập toán 11 - Cánh diều 2

Từ đồ thị, để tìm\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\), ta cần xác định khi \(x\) dần tới dương vô cực thì \(f\left( x \right)\) dần tới đâu. Tương tự với \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right)\).

Lời giải chi tiết

Từ đồ thị, ta nhận thấy rằng:

+ Khi \(x\) dần tới dương vô cực thì \(f\left( x \right)\) dần tới 1. Như vậy \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 1\).

+ Khi \(x\) dần tới âm vô cực thì \(f\left( x \right)\) dần tới 1. Như vậy \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 1\).

+ Khi \(x\) dần tới \( - 2\) về bên phải thì \(f\left( x \right)\) dần tới âm vô cực. Như vậy \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right) = - \infty \).

+ Khi \(x\) dần tới \( - 2\) về bên trái thì \(f\left( x \right)\) dần tới dương vô cực. Như vậy \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right) = + \infty \).

Giải bài 19 trang 76 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp

Bài 19 trang 76 sách bài tập Toán 11 Cánh Diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường xoay quanh việc tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số, tìm cực trị và vẽ đồ thị hàm số.

Nội dung chi tiết bài 19 trang 76 SBT Toán 11 Cánh Diều

Bài 19 thường bao gồm các dạng bài tập sau:

  • Dạng 1: Tìm đạo hàm của hàm số.
  • Dạng 2: Khảo sát hàm số bằng đạo hàm (xác định khoảng đồng biến, nghịch biến, cực trị).
  • Dạng 3: Giải các bài toán ứng dụng đạo hàm (tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số).

Hướng dẫn giải chi tiết từng phần của bài 19

Phần 1: Tìm đạo hàm

Để tìm đạo hàm của hàm số, học sinh cần nắm vững các quy tắc tính đạo hàm cơ bản như quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp. Ví dụ, nếu hàm số có dạng y = f(x) + g(x), thì đạo hàm của y là y' = f'(x) + g'(x).

Phần 2: Khảo sát hàm số bằng đạo hàm

Để khảo sát hàm số bằng đạo hàm, học sinh cần thực hiện các bước sau:

  1. Tính đạo hàm y'.
  2. Tìm tập xác định của hàm số.
  3. Giải phương trình y' = 0 để tìm các điểm cực trị.
  4. Lập bảng biến thiên của hàm số.
  5. Kết luận về khoảng đồng biến, nghịch biến, cực trị và giới hạn của hàm số.

Phần 3: Giải các bài toán ứng dụng đạo hàm

Khi giải các bài toán ứng dụng đạo hàm, học sinh cần xác định đúng đại lượng cần tìm (giá trị lớn nhất, giá trị nhỏ nhất) và sử dụng đạo hàm để tìm ra kết quả.

Ví dụ minh họa giải bài 19 trang 76 SBT Toán 11 Cánh Diều

Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Hãy khảo sát hàm số bằng đạo hàm.

Giải:

  1. Tính đạo hàm: y' = 3x2 - 6x.
  2. Giải phương trình y' = 0: 3x2 - 6x = 0 => x = 0 hoặc x = 2.
  3. Lập bảng biến thiên:
    4. x-∞02+∞
    y'+-+
    yNBĐBNB
  4. Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.

Lưu ý khi giải bài 19 trang 76 SBT Toán 11 Cánh Diều

  • Nắm vững các quy tắc tính đạo hàm.
  • Hiểu rõ ý nghĩa của đạo hàm trong việc khảo sát hàm số.
  • Lập bảng biến thiên một cách chính xác.
  • Kiểm tra lại kết quả sau khi giải bài.

Tusach.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các bạn học sinh sẽ tự tin hơn khi giải bài 19 trang 76 sách bài tập Toán 11 Cánh Diều. Chúc các bạn học tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN