Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 6 trang 10 sách bài tập toán 11 - Cánh diều
SBT Toán 11 - Cánh diều
SBT TOÁN TẬP 1 - CÁNH DIỀU
Chương I. Hàm số lượng giác và phương trình lượng giác
Bài 1. Góc lượng giác. Giá trị lượng giác của góc lượng giác

Giải bài 6 trang 10 sách bài tập toán 11 - Cánh diều

Giải bài 6 trang 10 SBT Toán 11 Cánh Diều

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài 6 trang 10 sách bài tập Toán 11 Cánh Diều. Chúng tôi hiểu rằng việc tự học và làm bài tập có thể gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tốt nhất để giúp bạn học tập hiệu quả.

Bài viết này sẽ cung cấp đáp án, phương pháp giải và những lưu ý quan trọng để bạn có thể tự tin giải quyết bài tập này.

Cho lục giác đều \(ABCDEF\)nội tiếp trong đường tròn lượng giác (thứ tự đi từ \(A\) đến các đỉnh theo chiều ngược chiều kim đồng hồ).

Đề bài

Cho lục giác đều \(ABCDEF\)nội tiếp trong đường tròn lượng giác (thứ tự đi từ \(A\) đến các đỉnh theo chiều ngược chiều kim đồng hồ). Tính số đo của các góc lượng giác \(\left( {OA,OB} \right)\), \(\left( {OA,OC} \right)\), \(\left( {OA,OD} \right)\), \(\left( {OA,OE} \right)\), \(\left( {OA,OF} \right)\).

Phương pháp giải - Xem chi tiếtGiải bài 6 trang 10 sách bài tập toán 11 - Cánh diều 1

Do lục giác đều \(ABCDEF\) nội tiếp trong đường tròn lượng giác tâm \(O\), nên ta có 6 góc bằng nhau: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = {60^o} = \frac{\pi }{3}\)

Sử dụng hệ thức Chasles để tính số đo của các góc lượng giác \(\left( {OA,OB} \right)\),\(\left( {OA,OC} \right)\), \(\left( {OA,OD} \right)\), \(\left( {OA,OE} \right)\), \(\left( {OA,OF} \right)\)

Lời giải chi tiết

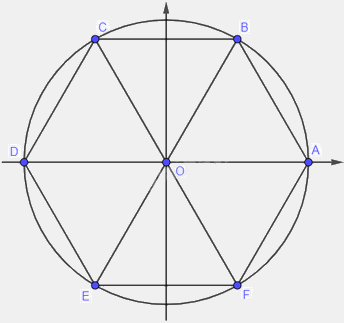
Giải bài 6 trang 10 sách bài tập toán 11 - Cánh diều 2

Vì lục giác đều \(ABCDEF\) nội tiếp đường tròn lượng giác tâm \(O\), nên ta có 6 góc bằng nhau: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = {60^o} = \frac{\pi }{3}\)

Do \(\widehat {AOB} = \frac{\pi }{3} \Rightarrow \left( {OA,OB} \right) = \frac{\pi }{3} + k2\pi \).

Áp dụng hệ thức Chasles, ta có:

\(\left( {OA,OC} \right) = \left( {OA,OB} \right) + \left( {OB,OC} \right) + k2\pi = \frac{\pi }{3} + \frac{\pi }{3} + k2\pi = \frac{{2\pi }}{3} + k2\pi \)

\(\left( {OA,OD} \right) = \left( {OA,OC} \right) + \left( {OC,OD} \right) + k2\pi = \frac{{2\pi }}{3} + \frac{\pi }{3} + k2\pi = \pi + k2\pi \)

\(\left( {OA,OE} \right) = \left( {OA,OD} \right) + \left( {OD,OE} \right) + k2\pi = \pi + \frac{\pi }{3} + k2\pi = \frac{{4\pi }}{3} + k2\pi = - \frac{{2\pi }}{3} + k2\pi \)

\(\left( {OA,OF} \right) = \left( {OA,OE} \right) + \left( {OE,OF} \right) + k2\pi = - \frac{{2\pi }}{3} + \frac{\pi }{3} + k2\pi = - \frac{\pi }{3} + k2\pi \)

Giải bài 6 trang 10 SBT Toán 11 Cánh Diều: Tổng quan và Hướng dẫn chi tiết

Bài 6 trang 10 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về hàm số lượng giác và đồ thị. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về các phép biến đổi lượng giác, tính chất của hàm số lượng giác và cách vẽ đồ thị để giải quyết các bài toán cụ thể.

Nội dung chính của bài 6 trang 10 SBT Toán 11 Cánh Diều

  • Phần 1: Bài tập về việc xác định tập xác định của hàm số lượng giác.
  • Phần 2: Bài tập về việc tìm tập giá trị của hàm số lượng giác.
  • Phần 3: Bài tập về việc xét tính chẵn lẻ của hàm số lượng giác.
  • Phần 4: Bài tập về việc vẽ đồ thị hàm số lượng giác.

Hướng dẫn giải chi tiết bài 6 trang 10 SBT Toán 11 Cánh Diều

Để giải quyết bài 6 trang 10 SBT Toán 11 Cánh Diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:

  1. Các phép biến đổi lượng giác cơ bản: Cộng, trừ, nhân, chia góc; công thức lượng giác cơ bản (sin, cos, tan, cot).
  2. Tính chất của hàm số lượng giác: Chu kỳ, tính chẵn lẻ, giá trị lớn nhất, giá trị nhỏ nhất.
  3. Cách vẽ đồ thị hàm số lượng giác: Xác định các điểm đặc biệt (điểm cực đại, điểm cực tiểu, điểm cắt trục).

Ví dụ minh họa:

Giả sử bài tập yêu cầu tìm tập xác định của hàm số y = tan(2x + π/3). Để giải bài này, bạn cần nhớ rằng hàm số tan(x) xác định khi x ≠ π/2 + kπ (k ∈ Z). Do đó, 2x + π/3 ≠ π/2 + kπ, suy ra 2x ≠ π/6 + kπ, và cuối cùng x ≠ π/12 + kπ/2 (k ∈ Z). Vậy tập xác định của hàm số là R \ {π/12 + kπ/2 | k ∈ Z}.

Các dạng bài tập thường gặp và phương pháp giải

Dưới đây là một số dạng bài tập thường gặp trong bài 6 trang 10 SBT Toán 11 Cánh Diều và phương pháp giải:

Dạng bài tậpPhương pháp giải
Tìm tập xác địnhXác định điều kiện để hàm số có nghĩa (ví dụ: mẫu số khác 0, biểu thức trong căn lớn hơn hoặc bằng 0).
Tìm tập giá trịSử dụng các tính chất của hàm số lượng giác (giá trị lớn nhất, giá trị nhỏ nhất) hoặc biến đổi hàm số về dạng đơn giản hơn.
Xét tính chẵn lẻKiểm tra xem f(-x) = f(x) (hàm chẵn) hay f(-x) = -f(x) (hàm lẻ).
Vẽ đồ thịXác định các điểm đặc biệt, vẽ các đoạn đồ thị và nối chúng lại.

Lưu ý khi giải bài tập

  • Luôn kiểm tra lại điều kiện xác định của hàm số.
  • Sử dụng máy tính bỏ túi để tính toán các giá trị lượng giác.
  • Vẽ đồ thị hàm số để kiểm tra lại kết quả.
  • Tham khảo các tài liệu tham khảo và bài giải mẫu để hiểu rõ hơn về cách giải bài tập.

Kết luận:

Bài 6 trang 10 SBT Toán 11 Cánh Diều là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số lượng giác và đồ thị. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết bài tập này một cách hiệu quả. Chúc bạn học tập tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN