Giải bài 5 trang 89 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 5 trang 89 Sách bài tập Toán 11 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 5 trang 89 sách bài tập Toán 11 Cánh Diều. Bài viết này cung cấp đáp án, cách giải và giải thích rõ ràng từng bước để giúp học sinh hiểu bài và làm bài tập một cách hiệu quả.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và dễ hiểu nhất, giúp các em học sinh nắm vững kiến thức Toán 11.
*: Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tính góc giữa hai đường thẳng AD và BC
Đề bài
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tính góc giữa hai đường thẳng AD và BC, biết \(MN = a\sqrt 3 \) và \(AD{\rm{ }} = {\rm{ }}BC = 2a.\)
Phương pháp giải - Xem chi tiết
Dựa vào các cách xác định góc giữa hai đường thẳng đã học để làm.
Lời giải chi tiết
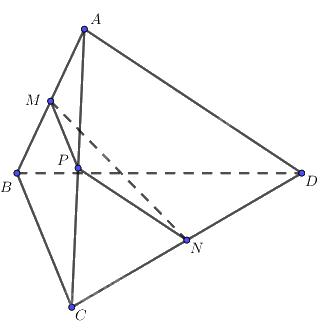
Gọi P là trung điểm của AC.
Ta có: MP, PN lần lượt là đường trung bình của \(\Delta ABC,\Delta ACD.\)
\( \Rightarrow MP//BC,{\rm{ }}PN//AD\) và \(MP = \frac{1}{2}BC = a,{\rm{ }}PN = \frac{1}{2}AD = a.\)
Do đó \(\left( {AD,BC} \right) = \left( {PN,MP} \right).\)
Xét \(\Delta MNP:\)
\(cos\widehat {MPN} = \frac{{M{P^2} + P{N^2} - M{N^2}}}{{2MP.PN}} = \frac{{{a^2} + {a^2} - {{\left( {a\sqrt 3 } \right)}^2}}}{{2a.a}} = - \frac{1}{2} \Rightarrow \widehat {MPN} = {120^0}.\)
Suy ra \(\left( {AD,BC} \right) = \left( {PN,MP} \right) = {180^0} - \widehat {MPN} = {180^0} - {120^0} = {60^0}.\)
Vậy góc giữa hai đường thẳng AD và BC là 600.
Giải bài 5 trang 89 Sách bài tập Toán 11 Cánh Diều: Tổng quan
Bài 5 trang 89 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về hàm số, đồ thị hàm số và các phép biến đổi hàm số để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh phân tích hàm số, xác định các yếu tố quan trọng như tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.
Nội dung chi tiết bài 5 trang 89 SBT Toán 11 Cánh Diều
Bài 5 thường bao gồm các dạng bài tập sau:
- Dạng 1: Xác định tập xác định của hàm số. Học sinh cần nắm vững các điều kiện để hàm số có nghĩa, ví dụ như mẫu số khác 0, biểu thức dưới dấu căn lớn hơn hoặc bằng 0, logarit có cơ số lớn hơn 0 và khác 1,...
- Dạng 2: Tìm tập giá trị của hàm số. Học sinh cần sử dụng các phương pháp như xét hàm số trên các khoảng, tìm giá trị lớn nhất và nhỏ nhất của hàm số, hoặc sử dụng đạo hàm để tìm tập giá trị.
- Dạng 3: Xét tính đơn điệu của hàm số. Học sinh cần tính đạo hàm của hàm số và xét dấu đạo hàm để xác định khoảng đồng biến và nghịch biến của hàm số.
- Dạng 4: Tìm cực trị của hàm số. Học sinh cần giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị của hàm số, sau đó xét dấu đạo hàm để xác định loại cực trị (cực đại hoặc cực tiểu).
- Dạng 5: Vẽ đồ thị hàm số. Học sinh cần xác định các yếu tố quan trọng của đồ thị hàm số như giao điểm với các trục tọa độ, tiệm cận, cực trị và vẽ đồ thị dựa trên các thông tin đó.
Lời giải chi tiết bài 5 trang 89 SBT Toán 11 Cánh Diều
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 5 trang 89 sách bài tập Toán 11 Cánh Diều:
Câu a)
(Giả sử đây là một hàm số cụ thể, ví dụ: y = x2 - 4x + 3)
Giải:
- Tập xác định: D = ℝ
- Tập giá trị: y ≥ -1
- Tính đơn điệu: Hàm số nghịch biến trên khoảng (-∞; 2) và đồng biến trên khoảng (2; +∞)
- Cực trị: Hàm số đạt cực tiểu tại x = 2, y = -1
- Đồ thị: (Mô tả cách vẽ đồ thị hàm số)
Câu b)
(Giả sử đây là một hàm số cụ thể, ví dụ: y = 1/x)
Giải:
- Tập xác định: D = ℝ \ {0}
- Tập giá trị: y ≠ 0
- Tính đơn điệu: Hàm số nghịch biến trên khoảng (-∞; 0) và (0; +∞)
- Không có cực trị
- Đồ thị: (Mô tả cách vẽ đồ thị hàm số)
Mẹo giải bài tập Toán 11 Cánh Diều hiệu quả
Để giải bài tập Toán 11 Cánh Diều hiệu quả, bạn nên:
- Nắm vững kiến thức cơ bản về hàm số, đồ thị hàm số và các phép biến đổi hàm số.
- Luyện tập thường xuyên các bài tập khác nhau để làm quen với các dạng bài tập và rèn luyện kỹ năng giải bài.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm vẽ đồ thị để kiểm tra lại kết quả và hiểu rõ hơn về đồ thị hàm số.
- Tham khảo các tài liệu tham khảo, sách giải bài tập hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè.
Kết luận
Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn khi giải bài 5 trang 89 sách bài tập Toán 11 Cánh Diều và đạt kết quả tốt trong môn Toán.
Tusach.vn luôn đồng hành cùng các em trên con đường học tập. Chúc các em học tốt!