Giải bài 31 trang 81 Sách bài tập Toán 11 Cánh Diều

Giải bài 31 trang 81 sách bài tập toán 11 - Cánh diều

Giải bài 31 trang 81 SBT Toán 11 Cánh Diều

Bài 31 trang 81 Sách bài tập Toán 11 Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 31 trang 81 SBT Toán 11 Cánh Diều, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.

Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam

Đề bài

Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có khối lượng đến 250 g như trong bảng sau:

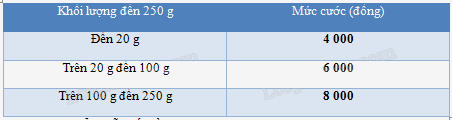
Giải bài 31 trang 81 sách bài tập toán 11 - Cánh diều 1

a) Hãy biểu diễn số tiền phải trả khi sử dụng dịch vụ thư cơ bản và bưu thiếp theo khối lượng của thư cơ bản và bưu thiếp.

b) Hàm số trên có liên tục trên tập xác định hay không?

Phương pháp giải - Xem chi tiết Giải bài 31 trang 81 sách bài tập toán 11 - Cánh diều 2

a) Dựa vào bảng, ta thấy với khối lượng từ 0 đến 20 g thì mức cước là 4000 đồng, từ trên 20 g đến 100 g thì mức cước là 6000 đồng, từ trên 100 g đến 250 g thì mức cước là 8000 đồng. Từ đó ta sẽ có hàm số biểu diễn số tiền phải trả khi sử dụng dịch vụ thư cơ bản và bưu thiếp theo khối lượng của thư cơ bản và bưu thiếp.

b) Hàm số có tập xác định là \(\left( {0,250} \right]\). Sử dụng các tính chất của hàm số liên tục.

Lời giải chi tiết

a) Dựa vào bảng, ta thấy với khối lượng từ 0 đến 20 g thì mức cước là 4000 đồng, từ trên 20 g đến 100 g thì mức cước là 6000 đồng, từ trên 100 g đến 250 g thì mức cước là 8000 đồng. Như vậy, nếu gọi\(x\) là khối lượng của thư cơ bản và bưu thiếp và \(f\left( x \right)\) là số tiền phải trả thì ta có hàm số: \(f\left( x \right) = \left\{ \begin{array}{l}4000{\rm{ }}\left( {0 < x \le 20} \right)\\6000{\rm{ }}\left( {20 < x \le 100} \right)\\8000{\rm{ }}\left( {100 < x \le 250} \right)\end{array} \right.\).

b) Hàm số có tập xác định là \(\left( {0,250} \right]\).

Ta có \(\mathop {\lim }\limits_{x \to {{20}^ - }} f\left( x \right) = 4000\) và \(\mathop {\lim }\limits_{x \to {{20}^ + }} f\left( x \right) = 6000\). Do \(\mathop {\lim }\limits_{x \to {{20}^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {{20}^ + }} f\left( x \right)\), nên không tồn tại \(\mathop {\lim }\limits_{x \to 20} f\left( x \right)\).

Suy ra hàm số không liên tục tại \(x = 20\).

Mà \(20 \in \left( {0,250} \right]\), ta kết luận hàm số không liên tục trên tập xác định của nó.

Giải bài 31 trang 81 Sách bài tập Toán 11 Cánh Diều: Tổng quan và Phương pháp giải

Bài 31 trang 81 Sách bài tập Toán 11 Cánh Diều thuộc chương trình học về đạo hàm của hàm số. Bài tập này thường yêu cầu học sinh:

Tính đạo hàm của hàm số tại một điểm.
Tìm đạo hàm của hàm số.
Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến, khoảng đơn điệu, cực trị,...

Để giải bài tập này hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:

Định nghĩa đạo hàm.
Các quy tắc tính đạo hàm (quy tắc cộng, trừ, nhân, chia, hàm hợp,...).
Đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit,...).

Lời giải chi tiết bài 31 trang 81 SBT Toán 11 Cánh Diều

Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài 31. Giả sử bài 31 yêu cầu tính đạo hàm của hàm số f(x) = x³ - 3x² + 2x - 1 tại x = 2.

Lời giải:

Ta có: f'(x) = 3x² - 6x + 2

Thay x = 2 vào f'(x), ta được: f'(2) = 3(2)² - 6(2) + 2 = 12 - 12 + 2 = 2

Vậy, đạo hàm của hàm số f(x) tại x = 2 là 2.

Các dạng bài tập tương tự và cách giải

Ngoài bài 31, còn rất nhiều bài tập tương tự trong sách bài tập Toán 11 Cánh Diều. Dưới đây là một số dạng bài tập thường gặp và cách giải:

Bài tập tính đạo hàm: Sử dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm của hàm số.
Bài tập tìm tiếp tuyến: Sử dụng công thức phương trình tiếp tuyến của đường cong tại một điểm.
Bài tập xét tính đơn điệu: Tính đạo hàm f'(x) và xét dấu của f'(x) để xác định khoảng đơn điệu của hàm số.
Bài tập tìm cực trị: Giải phương trình f'(x) = 0 để tìm các điểm cực trị của hàm số.

Mẹo giải bài tập đạo hàm hiệu quả

Nắm vững các quy tắc tính đạo hàm.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
Tham khảo các tài liệu tham khảo, sách giải bài tập để hiểu rõ hơn về các kiến thức liên quan.

Tusach.vn – Nguồn tài liệu học Toán 11 uy tín

Tusach.vn là một website cung cấp đầy đủ các tài liệu học Toán 11, bao gồm:

Giải bài tập sách giáo khoa.
Giải bài tập sách bài tập.
Đề thi thử.
Các bài viết hướng dẫn, tổng hợp kiến thức.

Hãy truy cập Tusach.vn để học Toán 11 hiệu quả hơn!

Chương	Nội dung chính
Đạo hàm	Định nghĩa, quy tắc tính đạo hàm, ứng dụng của đạo hàm
Giới hạn	Định nghĩa, tính chất của giới hạn