Giải bài 48 trang 110 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 48 trang 110 SBT Toán 11 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 48 trang 110 sách bài tập Toán 11 Cánh Diều. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những nội dung chất lượng, chính xác và cập nhật nhất để hỗ trợ học sinh trong quá trình học tập.
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật, \(AB = 2a\), \(AD = 3a\)
Đề bài
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật, \(AB = 2a\), \(AD = 3a\), tam giác \(\left( {SAB} \right)\) vuông cân tại \(S\) và nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right)\). Tính khoảng cách:
a) Từ điểm \(C\) đến mặt phẳng \(\left( {SAB} \right)\).
b) Giữa hai đường thẳng \(SB\) và \(CD\).
c) Giữa hai đường thẳng \(BC\) và \(SA\).
d) Từ điểm \(S\) đến mặt phẳng \(\left( {ABCD} \right)\).
Phương pháp giải - Xem chi tiết
a) Gọi \(H\) là trung điểm của \(AB\). Chứng minh rằng \(SH \bot \left( {ABCD} \right)\)và chỉ ra rằng \(B\) là hình chiếu của \(C\) trên mặt phẳng \(\left( {SAB} \right)\), từ đó khoảng cách cần tính là đoạn thẳng \(BC\).
b) Chỉ ra rằng do \(CD\parallel \left( {SAB} \right)\), và \(SB \subset \left( {SBC} \right)\), nên khoảng cách giữa hai đường thẳng \(SB\) và \(CD\) cũng chính là khoảng cách giữa \(CD\) và \(\left( {SBC} \right)\), và cũng bằng đoạn thẳng \(BC\).
c) Chi ra rằng \(SB\) là đường vuông góc chung của 2 đường thẳng \(SA\) và \(BC\), từ đó chứng minh được khoảng cách này bằng đoạn thẳng \(SB\).
d) Theo câu a, ta có \(SH \bot \left( {ABCD} \right)\) từ đó khoảng cách cần tính là đoạn thẳng \(SH\).
Lời giải chi tiết
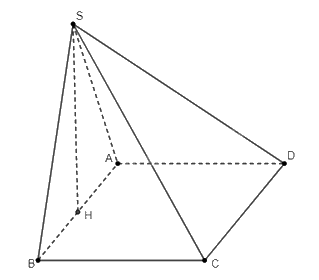
a) Gọi \(H\) là trung điểm của \(AB\). Do tam giác \(SAB\) vuông cân tại \(S\) nên ta có \(SA \bot SB\) và \(SH \bot AB\). Hơn nữa, do \(\left( {SAB} \right) \bot \left( {ABCD} \right)\) và \(AB\) là giao tuyến của 2 mặt phẳng đó, ta suy ra \(SH \bot \left( {ABCD} \right)\). Từ đó \(SH \bot BC\).
Do \(ABCD\) là hình chữ nhật, ta suy ra \(AB \bot BC\). Như vậy, do \(SH \bot BC\), \(AB \bot BC\) ta suy ra \(\left( {SAB} \right) \bot BC\). Như vậy \(B\) là hình chiếu của \(C\) trên mặt phẳng \(\left( {SAB} \right)\), từ đó khoảng cách cần tính là đoạn thẳng \(BC\). Mà \(BC = 3a\), nên khoảng cách từ điểm \(C\) đến \(\left( {SAB} \right)\) là \(3a\).
b) Do \(ABCD\) là hình chữ nhật, ta suy ra \(CD\parallel AB\), mà \(AB \subset \left( {SAB} \right)\) nên \(CD\parallel \left( {SAB} \right)\). Hơn nữa, do \(SB \subset \left( {SBC} \right)\), nên khoảng cách giữa hai đường thẳng \(SB\) và \(CD\) cũng chính là khoảng cách giữa \(CD\) và \(\left( {SBC} \right)\), và nó cũng bằng khoảng cách từ điểm \(C\) đến \(\left( {SBC} \right)\). Theo câu a, khoảng cách này chính là đoạn thẳng \(BC\), tức là khoảng cách giữa hai đường thẳng \(SB\) và \(CD\) bằng \(3a\).
c) Theo câu a, ta có \(SA \bot SB\). Hơn nữa, ta cũng có \(\left( {SAB} \right) \bot BC\) nên \(SB \bot BC\). Như vậy, \(SB\) là đường vuông góc chung của 2 đường thẳng \(SA\) và \(BC\), điều này có nghĩa khoảng cách giữa \(SA\) và \(BC\) là đoạn thẳng \(SB\).
Tam giác \(SAB\) vuông cân tại \(S\) nên ta có \(A{B^2} = 2S{B^2} \Rightarrow SB = \frac{{AB}}{{\sqrt 2 }}\)
Mà \(AB = 2a\) nên \(SB = \frac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \).
Vậy khoảng cách giữa \(SA\) và \(BC\) là \(a\sqrt 2 \).
d) Theo câu a, ta có \(SH \bot \left( {ABCD} \right)\). Điều này có nghĩa khoảng cách từ \(S\) đến \(\left( {ABCD} \right)\) là đoạn thẳng \(SH\).
Tam giác \(SAB\) vuông cân tại \(S\) có đường trung tuyến \(SH\) nên ta có \(SH = \frac{{AB}}{2} = \frac{{2a}}{2} = a\).
Vậy khoảng cách từ \(S\) đến \(\left( {ABCD} \right)\) là \(a\).
Giải bài 48 trang 110 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải
Bài 48 trang 110 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng để giải quyết các bài toán thực tế.
Nội dung chi tiết bài 48 trang 110 SBT Toán 11 Cánh Diều
Bài 48 thường bao gồm các dạng bài tập sau:
- Xác định mối quan hệ giữa đường thẳng và mặt phẳng: Kiểm tra xem một đường thẳng có song song, vuông góc hay cắt một mặt phẳng hay không.
- Chứng minh tính song song, vuông góc: Sử dụng các định lý, tính chất để chứng minh mối quan hệ giữa đường thẳng và mặt phẳng.
- Tính góc giữa đường thẳng và mặt phẳng: Áp dụng công thức tính góc để tìm góc cần tìm.
- Tìm giao điểm của đường thẳng và mặt phẳng: Xác định vị trí giao điểm (nếu có) của đường thẳng và mặt phẳng.
Lời giải chi tiết bài 48 trang 110 SBT Toán 11 Cánh Diều
Dưới đây là lời giải chi tiết cho từng phần của bài 48 trang 110 SBT Toán 11 Cánh Diều:
Câu a: (Ví dụ minh họa - cần thay thế bằng nội dung thực tế của bài toán)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD). Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Lời giải:
- Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông nên AC ⊥ BD.
- Vì SA ⊥ (ABCD) nên SA ⊥ AC.
- Suy ra AC ⊥ (SAC). Do đó, góc giữa SC và mặt phẳng (ABCD) bằng góc SCA.
- Tính AC = a√2. Trong tam giác SAC vuông tại A, ta có tan SCA = SA/AC = SA/(a√2).
- Vậy, góc SCA = arctan(SA/(a√2)).
Câu b: (Ví dụ minh họa - cần thay thế bằng nội dung thực tế của bài toán)
Chứng minh rằng nếu một đường thẳng vuông góc với một trong hai đường thẳng nằm trong một mặt phẳng thì nó không vuông góc với mặt phẳng đó.
Lời giải:
Giả sử đường thẳng d vuông góc với đường thẳng a nằm trong mặt phẳng (P). Nếu d vuông góc với (P) thì d phải vuông góc với mọi đường thẳng nằm trong (P). Nhưng a nằm trong (P) nên d phải vuông góc với a. Điều này mâu thuẫn với giả thiết d vuông góc với a. Vậy, d không vuông góc với (P).
Mẹo giải bài tập về đường thẳng và mặt phẳng
- Vẽ hình: Vẽ hình chính xác và trực quan là bước quan trọng để hiểu rõ bài toán.
- Nắm vững định lý: Ghi nhớ và vận dụng linh hoạt các định lý, tính chất về quan hệ song song, vuông góc.
- Sử dụng phương pháp tọa độ: Trong một số trường hợp, phương pháp tọa độ có thể giúp giải quyết bài toán một cách dễ dàng hơn.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong sách bài tập Toán 11 Cánh Diều. Hãy truy cập Tusach.vn để tìm kiếm lời giải cho các bài tập khác và nâng cao kiến thức Toán 11 của bạn!
| Chương | Bài | Liên kết |
|---|---|---|
| 1 | Bài 1 | Link đến bài 1 |
| 2 | Bài 2 | Link đến bài 2 |