Giải bài 58 trang 118 Toán 11 Cánh Diều - Chi tiết, nhanh chóng

Giải bài 58 trang 118 sách bài tập toán 11 - Cánh diều

Giải bài 58 trang 118 sách bài tập Toán 11 Cánh Diều

Chào mừng các em học sinh đến với lời giải chi tiết bài 58 trang 118 SBT Toán 11 Cánh Diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về nội dung bài học.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.

Cho tứ diện \(ABCD\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(AB\), \(AD\); \(P\), \(Q\)

Đề bài

Cho tứ diện \(ABCD\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(AB\), \(AD\); \(P\), \(Q\) lần lượt thuộc các cạnh \(CD\), \(BC\) (\(P\), \(Q\) không là trung điểm của \(CD\), \(BC\)). Chứng minh rằng nếu \(M\), \(N\), \(P\), \(Q\) cùng thuộc một mặt phẳng thì ba đường thẳng \(MQ\), \(NP\) và \(AC\) cùng đi qua một điểm.

Phương pháp giải - Xem chi tiết Giải bài 58 trang 118 sách bài tập toán 11 - Cánh diều 1

Gọi \(I\) là giao điểm của \(NP\) và \(AC\). Ta suy ra rằng \(I\) nằm trên giao tuyến của \(\left( {MNPQ} \right)\) và \(\left( {ABC} \right)\), từ đó suy ra \(I \in MQ\) và điều phải chứng minh.

Lời giải chi tiết

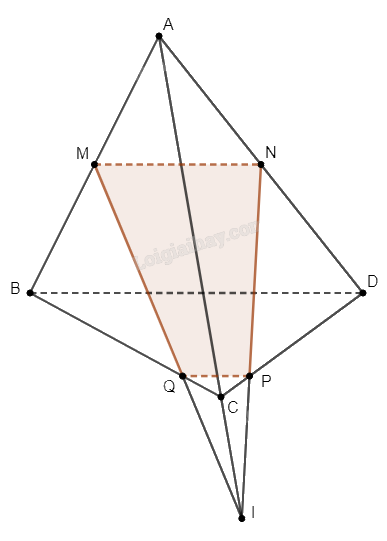
Giải bài 58 trang 118 sách bài tập toán 11 - Cánh diều 2

Xét \(\left( {ADC} \right)\), do \(P\) không là trung điểm của \(CD\), nên đường thẳng \(NP\) cắt đường thẳng \(AC\). Gọi \(I\) là giao điểm của \(NP\) và \(AC\).

Ta có \(I \in \left( {MNPQ} \right)\) (do \(I\) nằm trên \(NP\)) và \(I \in \left( {ABC} \right)\) (do \(I\) nằm trên \(AC\)). Như vậy \(I\) nằm trên giao tuyến của \(\left( {MNPQ} \right)\) và \(\left( {ABC} \right)\).

Ta nhận thấy rằng \(\left\{ \begin{array}{l}M \in \left( {MNPQ} \right)\\M \in AB \subset \left( {ABC} \right)\end{array} \right. \Rightarrow M \in \left( {MNPQ} \right) \cap \left( {ABC} \right)\), và

\(\left\{ \begin{array}{l}Q \in \left( {MNPQ} \right)\\Q \in BC \subset \left( {ABC} \right)\end{array} \right. \Rightarrow Q \in \left( {MNPQ} \right) \cap \left( {ABC} \right)\).

Do đó giao tuyến của \(\left( {MNPQ} \right)\) và \(\left( {ABC} \right)\) là đường thẳng \(MQ\).

Mà \(I\) nằm trên giao tuyến của \(\left( {MNPQ} \right)\) và \(\left( {ABC} \right)\), nên \(I \in MQ\).

Vậy \(MQ\), \(NP\) và \(AC\) cùng đi qua điểm \(I\).

Bài toán được chứng minh.

Giải bài 58 trang 118 sách bài tập Toán 11 Cánh Diều: Tổng quan

Bài 58 trang 118 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về Đường thẳng và mặt phẳng trong không gian. Bài tập này thường tập trung vào việc vận dụng các kiến thức về:

Quan hệ song song giữa đường thẳng và mặt phẳng: Xác định điều kiện để một đường thẳng song song với một mặt phẳng.
Quan hệ vuông góc giữa đường thẳng và mặt phẳng: Xác định điều kiện để một đường thẳng vuông góc với một mặt phẳng.
Góc giữa đường thẳng và mặt phẳng: Tính góc giữa một đường thẳng và mặt phẳng.
Khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ một điểm đến một mặt phẳng.

Giải chi tiết bài 58 trang 118 SBT Toán 11 Cánh Diều

Để giải bài 58 trang 118 SBT Toán 11 Cánh Diều một cách hiệu quả, các em cần nắm vững các định nghĩa, tính chất và công thức liên quan đến quan hệ giữa đường thẳng và mặt phẳng trong không gian. Dưới đây là hướng dẫn giải chi tiết cho từng câu hỏi trong bài tập:

Câu a)

(Nội dung câu a và lời giải chi tiết)

Ví dụ: Cho hình chóp S.ABCD, đáy ABCD là hình vuông. Gọi M là trung điểm của CD. Chứng minh rằng AM vuông góc với mặt phẳng (SCD).

Lời giải:

Chứng minh AM vuông góc với CD.
Chứng minh CD vuông góc với mặt phẳng (SAM).
Suy ra CD vuông góc với SM.
Kết luận AM vuông góc với mặt phẳng (SCD).

Câu b)

(Nội dung câu b và lời giải chi tiết)

Câu c)

(Nội dung câu c và lời giải chi tiết)

Mẹo giải bài tập quan hệ giữa đường thẳng và mặt phẳng

Để giải các bài tập về quan hệ giữa đường thẳng và mặt phẳng, các em có thể áp dụng một số mẹo sau:

Vẽ hình: Vẽ hình chính xác và trực quan sẽ giúp các em dễ dàng hình dung được bài toán và tìm ra hướng giải.
Sử dụng các định lý: Nắm vững các định lý về quan hệ giữa đường thẳng và mặt phẳng để áp dụng vào giải bài tập.
Phân tích bài toán: Phân tích bài toán để xác định các yếu tố cần tìm và các mối quan hệ giữa chúng.
Sử dụng phương pháp tọa độ: Trong một số trường hợp, phương pháp tọa độ có thể giúp các em giải bài tập một cách dễ dàng hơn.

Luyện tập thêm

Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các trang web học tập trực tuyến.

Kết luận

Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em đã hiểu rõ hơn về cách giải bài 58 trang 118 sách bài tập Toán 11 Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!

Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với Tusach.vn để được hỗ trợ nhé!