Logo

Giải bài 40 trang 104 sách bài tập toán 11 - Cánh diều

Tổng quan nội dung

Giải bài 40 trang 104 SBT Toán 11 Cánh Diều

Tusach.vn cung cấp lời giải chi tiết và dễ hiểu bài 40 trang 104 sách bài tập Toán 11 Cánh Diều. Bài viết này sẽ giúp học sinh nắm vững kiến thức và kỹ năng giải toán, chuẩn bị tốt cho các kỳ thi sắp tới.

Chúng tôi luôn cập nhật đáp án nhanh chóng và chính xác nhất, đồng thời cung cấp các phương pháp giải bài tập hiệu quả.

Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\) và \(ABCD\) là hình chữ nhật. Chứng minh rằng:

Đề bài

Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\) và \(ABCD\) là hình chữ nhật. Chứng minh rằng:

a) \(\left( {SAB} \right) \bot \left( {SBC} \right)\)

b) \(\left( {SAD} \right) \bot \left( {SCD} \right)\)

Phương pháp giải - Xem chi tiếtGiải bài 40 trang 104 sách bài tập toán 11 - Cánh diều 1

Để chứng minh 2 mặt phẳng vuông góc, ta cần chứng minh 1 đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia.

Lời giải chi tiết

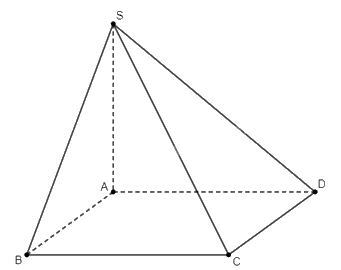
Giải bài 40 trang 104 sách bài tập toán 11 - Cánh diều 2

a) Do \(SA \bot \left( {ABCD} \right)\), ta suy ra \(SA \bot BC\).

Do \(ABCD\) là hình chữ nhật, ta suy ra \(AB \bot BC\).

Như vậy ta có \(SA \bot BC\), \(AB \bot BC\). Điều này dẫn tới \(\left( {SAB} \right) \bot BC\).

Do \(BC \subset \left( {SBC} \right)\), nên ta suy ra \(\left( {SAB} \right) \bot \left( {SBC} \right)\). Ta có điều phải chứng minh.

b) Do \(SA \bot \left( {ABCD} \right)\), ta suy ra \(SA \bot DC\).

Do \(ABCD\) là hình chữ nhật, ta suy ra \(AD \bot DC\).

Như vậy ta có \(SA \bot DC\), \(AD \bot DC\). Điều này dẫn tới \(\left( {SAD} \right) \bot DC\).

Do \(DC \subset \left( {SDC} \right)\), nên ta suy ra \(\left( {SAD} \right) \bot \left( {SDC} \right)\). Ta có điều phải chứng minh.

Giải bài 40 trang 104 SBT Toán 11 Cánh Diều: Tổng quan

Bài 40 trang 104 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về Đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit và các phép toán trên hàm số (tổng, hiệu, tích, thương, hàm hợp).

Nội dung chi tiết bài 40 trang 104 SBT Toán 11 Cánh Diều

Để giải quyết bài 40 trang 104 SBT Toán 11 Cánh Diều một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:

  • Các quy tắc tính đạo hàm: Đạo hàm của hàm số f(x) + g(x), f(x) - g(x), f(x) * g(x), f(x) / g(x), và đạo hàm của hàm hợp g(f(x)).
  • Đạo hàm của các hàm số cơ bản: Đạo hàm của xn, sin(x), cos(x), tan(x), cot(x), ex, ln(x).
  • Kỹ năng biến đổi đại số: Để đơn giản hóa biểu thức trước khi tính đạo hàm.

Hướng dẫn giải chi tiết bài 40 trang 104 SBT Toán 11 Cánh Diều

Dưới đây là hướng dẫn giải chi tiết từng phần của bài 40 trang 104 SBT Toán 11 Cánh Diều. (Lưu ý: Nội dung cụ thể của bài tập sẽ được trình bày chi tiết tại đây, ví dụ:)

Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1

Giải:

  1. Áp dụng quy tắc đạo hàm của tổng: f'(x) = (3x2)' + (2x)' + (-1)'
  2. Áp dụng quy tắc đạo hàm của hàm số lũy thừa: (3x2)' = 6x
  3. Áp dụng quy tắc đạo hàm của hàm số tuyến tính: (2x)' = 2
  4. Đạo hàm của hằng số bằng 0: (-1)' = 0
  5. Vậy, f'(x) = 6x + 2

Ví dụ 2: Tính đạo hàm của hàm số g(x) = sin(x) * cos(x)

Giải:

Áp dụng quy tắc đạo hàm của tích: g'(x) = (sin(x))' * cos(x) + sin(x) * (cos(x))'

Ta có: (sin(x))' = cos(x) và (cos(x))' = -sin(x)

Vậy, g'(x) = cos(x) * cos(x) + sin(x) * (-sin(x)) = cos2(x) - sin2(x)

Mẹo giải nhanh bài tập đạo hàm

Để giải nhanh các bài tập về đạo hàm, bạn có thể áp dụng các mẹo sau:

  • Nắm vững các công thức đạo hàm cơ bản: Điều này giúp bạn tiết kiệm thời gian và tránh sai sót.
  • Sử dụng bảng đạo hàm: Bảng đạo hàm là một công cụ hữu ích để tra cứu nhanh các công thức đạo hàm.
  • Luyện tập thường xuyên: Càng luyện tập nhiều, bạn càng trở nên thành thạo và tự tin hơn trong việc giải các bài tập về đạo hàm.

Tài liệu tham khảo thêm

Để hiểu sâu hơn về đạo hàm, bạn có thể tham khảo các tài liệu sau:

  • Sách giáo khoa Toán 11
  • Sách bài tập Toán 11
  • Các trang web học toán trực tuyến uy tín

Kết luận

Bài 40 trang 104 SBT Toán 11 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với hướng dẫn chi tiết và các mẹo giải nhanh trên, các bạn học sinh sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các bạn học tốt!