Giải bài 61 trang 31 SBT Toán 11 Cánh Diều

Giải bài 61 trang 31 sách bài tập toán 11 - Cánh diều

Giải bài 61 trang 31 SBT Toán 11 Cánh Diều

Tusach.vn xin giới thiệu lời giải chi tiết bài 61 trang 31 sách bài tập Toán 11 Cánh Diều. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cố gắng cung cấp những nội dung chất lượng, chính xác và cập nhật nhất để hỗ trợ học sinh trong quá trình học tập.

Dùng đồ thị hàm số \(y = \sin x\), \(y = \cos x\) để xác định số nghiệm của phương trình:

Đề bài

Dùng đồ thị hàm số \(y = \sin x\), \(y = \cos x\) để xác định số nghiệm của phương trình:

a) \(5\sin x - 3 = 0\) trên đoạn \(\left[ { - \pi ;4\pi } \right]\)

b) \(\sqrt 2 \cos x + 1 = 0\) trên khoảng \(\left( { - 4\pi ;0} \right)\)

Phương pháp giải - Xem chi tiết Giải bài 61 trang 31 sách bài tập toán 11 - Cánh diều 1

a) Biến đổi phương trình thành \(\sin x = \frac{3}{5}\).

Vẽ đồ thị hàm số \(y = \sin x\), đường thẳng \(y = \frac{3}{5}\) và đếm số giao điểm có hoành độ thuộc đoạn \(\left[ { - \pi ;4\pi } \right]\)

b) Biến đổi phương trình thành \(\cos x = \frac{{ - 1}}{{\sqrt 2 }}\).

Vẽ đồ thị hàm số \(y = \cos x\), đường thẳng \(y = \frac{{ - 1}}{{\sqrt 2 }}\) và đếm số giao điểm có hoành độ thuộc khoảng \(\left( { - 4\pi ;0} \right)\)

Lời giải chi tiết

a) Ta có \(5\sin x - 3 = 0 \Leftrightarrow \sin x = \frac{3}{5}\).

Nghiệm của phương trình trên chính là hoành độ các giao điểm của đường thẳng \(y = \frac{3}{5}\) và đồ thị hàm số \(y = \sin x\) như hình vẽ dưới đây.

Giải bài 61 trang 31 sách bài tập toán 11 - Cánh diều 2

Dựa vào hình vẽ, ta thấy đường thẳng \(y = \frac{3}{5}\) cắt đồ thị hàm số \(y = \sin x\) tại 4 điểm có hoành độ nằm trên đoạn \(\left[ { - \pi ;4\pi } \right]\). Có nghĩa là, phương trình \(5\sin x - 3 = 0\) có 4 nghiệm trên đoạn \(\left[ { - \pi ;4\pi } \right]\).

b) Ta có \(\sqrt 2 \cos x + 1 = 0 \Leftrightarrow \cos x = \frac{{ - 1}}{{\sqrt 2 }}\)

Nghiệm của phương trình trên chính là hoành độ các giao điểm của đường thẳng \(y = \frac{{ - 1}}{{\sqrt 2 }}\) và đồ thị hàm số \(y = \cos x\) như hình vẽ dưới đây.

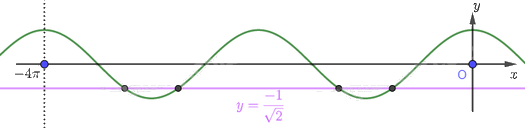
Giải bài 61 trang 31 sách bài tập toán 11 - Cánh diều 3

Dựa vào hình vẽ, ta thấy đường thẳng \(y = \frac{{ - 1}}{{\sqrt 2 }}\) cắt đồ thị hàm số \(y = \cos x\) tại 4 điểm có hoành độ nằm trên khoảng \(\left( { - 4\pi ;0} \right)\). Có nghĩa là, phương trình \(\sqrt 2 \cos x + 1 = 0\) có 4 nghiệm trên khoảng \(\left( { - 4\pi ;0} \right)\).

Giải bài 61 trang 31 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải

Bài 61 trang 31 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các công thức liên quan.

Nội dung bài toán

Bài 61 thường yêu cầu học sinh thực hiện các thao tác như:

Tìm tọa độ của một điểm hoặc vectơ.
Chứng minh đẳng thức vectơ.
Tính độ dài của vectơ.
Xác định mối quan hệ giữa các vectơ (cùng phương, cùng chiều, vuông góc).
Áp dụng kiến thức vectơ để giải quyết các bài toán hình học.

Phương pháp giải

Để giải bài 61 trang 31 SBT Toán 11 Cánh Diều, học sinh có thể áp dụng các phương pháp sau:

Sử dụng định nghĩa và tính chất của vectơ: Nắm vững định nghĩa vectơ, các phép toán vectơ (cộng, trừ, nhân với một số) và các tính chất của chúng.
Sử dụng tọa độ của vectơ: Biểu diễn vectơ bằng tọa độ và sử dụng các công thức tính toán liên quan đến tọa độ vectơ.
Sử dụng các công thức hình học: Áp dụng các công thức hình học (ví dụ: công thức tính độ dài đoạn thẳng, công thức tính diện tích tam giác) để giải quyết bài toán.
Phân tích bài toán: Chia bài toán thành các bước nhỏ hơn và giải quyết từng bước một.

Lời giải chi tiết bài 61 trang 31 SBT Toán 11 Cánh Diều

(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích và kết luận. Ví dụ:)

Bài 61: Cho tam giác ABC có A(1;2), B(3;4), C(-1;0). Tìm tọa độ của điểm D sao cho ABCD là hình bình hành.

Giải:

Vì ABCD là hình bình hành nên AB = DC và AB // DC. Gọi D(x;y). Ta có:

AB = (3-1; 4-2) = (2;2)
DC = (-1-x; 0-y) = (-1-x; -y)

Do AB = DC nên:

2 = -1 - x => x = -3

2 = -y => y = -2

Vậy D(-3; -2).

Luyện tập và Bài tập tương tự

Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Tusach.vn sẽ tiếp tục cập nhật thêm nhiều bài giải chi tiết và các dạng bài tập khác để hỗ trợ học sinh học tập tốt hơn.

Tusach.vn - Đồng hành cùng học sinh

Tusach.vn là website cung cấp lời giải bài tập Toán, Lý, Hóa, Sinh, Anh,... từ lớp 6 đến lớp 12. Chúng tôi luôn nỗ lực để mang đến cho học sinh những tài liệu học tập chất lượng, chính xác và dễ hiểu. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!

Chương	Bài	Nội dung
Vectơ trong không gian	61	Giải bài tập về hình bình hành, tính chất vectơ

Giải bài 61 trang 31 sách bài tập toán 11 - Cánh diều

Giải bài 61 trang 31 SBT Toán 11 Cánh Diều

Giải bài 61 trang 31 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải

Nội dung bài toán

Phương pháp giải

Lời giải chi tiết bài 61 trang 31 SBT Toán 11 Cánh Diều

Luyện tập và Bài tập tương tự

Tusach.vn - Đồng hành cùng học sinh

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN