Giải bài 4 trang 94 SBT Toán 11 Cánh Diều

Giải bài 4 trang 94 sách bài tập toán 11 - Cánh diều

Giải bài 4 trang 94 sách bài tập Toán 11 Cánh Diều

Tusach.vn xin giới thiệu lời giải chi tiết bài 4 trang 94 SBT Toán 11 Cánh Diều. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cố gắng cung cấp những tài liệu học tập chất lượng nhất để hỗ trợ các em học sinh học tập tốt hơn.

Cho tứ diện \(ABCD\). Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AB,{\rm{ }}CD\).

Đề bài

Cho tứ diện \(ABCD\). Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AB,{\rm{ }}CD\). Chứng minh rằng bốn điểm \(M,{\rm{ }}N,{\rm{ }}C,{\rm{ }}D\) không cùng nằm trong một mặt phẳng.

Phương pháp giải - Xem chi tiết Giải bài 4 trang 94 sách bài tập toán 11 - Cánh diều 1

Giả sử 4 điểm \(M\), \(N\), \(C\), \(D\) cùng nằm trong một mặt phẳng.

Từ đó chứng minh rằng \(M \in \left( {BCD} \right)\), suy ra \(A \in \left( {BCD} \right)\) và suy ra điều vô lí.

Lời giải chi tiết

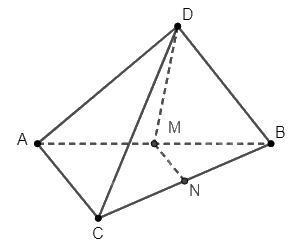
Giải bài 4 trang 94 sách bài tập toán 11 - Cánh diều 2

Do \(N\) là trung điểm của \(BC\), nên 4 điểm \(B\), \(N\), \(C\), \(D\) cùng nằm trong mặt phẳng.

Giả sử 4 điểm \(M\), \(N\), \(C\), \(D\) cùng nằm trong một mặt phẳng.

Điều này có nghĩa là \(M \in \left( {NCD} \right)\).

Do bốn điểm \(B\), \(N\), \(C\), \(D\) cùng nằm trong mặt phẳng, ta suy ra \(M \in \left( {BCD} \right)\).

Điểm \(M\) và điểm \(B\) cùng nằm trong mặt phẳng \(\left( {BCD} \right)\), nên \(BM \subset \left( {BCD} \right)\).

Mặt khác, do \(M\) là trung điểm của \(AB\), nên \(A \in BM\).

Suy ra \(A \in \left( {BCD} \right)\). Điều này là vô lí do \(ABCD\) là tứ diện nên bốn điểm \(A\), \(B\), \(C\), \(D\) không cùng nằm trong một mặt phẳng.

Giải bài 4 trang 94 SBT Toán 11 Cánh Diều: Tổng quan và Hướng dẫn chi tiết

Bài 4 trang 94 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về phép biến hình, đặc biệt là phép tịnh tiến, phép quay, và phép đối xứng để giải quyết các bài toán hình học.

Nội dung bài tập 4 trang 94 SBT Toán 11 Cánh Diều

Bài tập 4 thường yêu cầu học sinh:

Xác định ảnh của một điểm, một đường thẳng, một hình qua phép biến hình cho trước.
Tìm tâm, góc, và tỉ số của phép biến hình.
Chứng minh một đẳng thức liên quan đến các phép biến hình.
Vận dụng các phép biến hình để giải quyết các bài toán hình học phức tạp.

Phương pháp giải bài tập 4 trang 94 SBT Toán 11 Cánh Diều

Để giải quyết hiệu quả bài tập 4, học sinh cần nắm vững các kiến thức sau:

Khái niệm về phép biến hình: Hiểu rõ định nghĩa, tính chất của phép tịnh tiến, phép quay, phép đối xứng trục, phép đối xứng tâm.
Biểu thức của phép biến hình: Nắm vững công thức biểu diễn phép biến hình trong hệ tọa độ.
Tính chất bảo toàn của phép biến hình: Biết rằng phép biến hình bảo toàn khoảng cách, góc, và diện tích.
Ứng dụng của phép biến hình: Sử dụng phép biến hình để giải quyết các bài toán hình học một cách đơn giản và hiệu quả.

Giải chi tiết bài 4 trang 94 SBT Toán 11 Cánh Diều (Ví dụ minh họa)

Bài 4: Cho điểm A(1; 2) và đường thẳng d: x + y - 3 = 0. Tìm ảnh của điểm A và đường thẳng d qua phép tịnh tiến theo vectơ v = (2; -1).

Giải:

Ảnh của điểm A: Gọi A' là ảnh của A qua phép tịnh tiến theo vectơ v. Khi đó, tọa độ của A' là: A'(1 + 2; 2 - 1) = A'(3; 1).
Ảnh của đường thẳng d: Gọi d' là ảnh của d qua phép tịnh tiến theo vectơ v. Mỗi điểm M(x; y) thuộc d sẽ được biến thành điểm M'(x + 2; y - 1) thuộc d'. Thay x = x' - 2 và y = y' + 1 vào phương trình d, ta được: (x' - 2) + (y' + 1) - 3 = 0 ⇔ x' + y' - 4 = 0. Vậy phương trình của d' là: x + y - 4 = 0.

Lưu ý khi giải bài tập 4 trang 94 SBT Toán 11 Cánh Diều

Để đạt kết quả tốt nhất, học sinh nên:

Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Vẽ hình minh họa để hình dung rõ hơn về bài toán.
Sử dụng các công thức và tính chất của phép biến hình một cách chính xác.
Kiểm tra lại kết quả sau khi giải xong.

Tài liệu tham khảo hữu ích

Ngoài sách bài tập, học sinh có thể tham khảo thêm:

Sách giáo khoa Toán 11.
Các bài giảng trực tuyến về phép biến hình.
Các trang web và diễn đàn học tập trực tuyến.

Tusach.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải bài tập 4 trang 94 SBT Toán 11 Cánh Diều. Chúc các em học tập tốt!