Giải bài 32 trang 108 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 32 trang 108 SBT Toán 11 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 32 trang 108 sách bài tập Toán 11 Cánh Diều. Bài giải này được xây dựng dựa trên chương trình học và đáp án chính thức của Bộ Giáo dục và Đào tạo.
Chúng tôi luôn cố gắng cung cấp những lời giải dễ hiểu, chính xác và đầy đủ nhất để giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho \(a\), \(b\) là hai đường thẳng phân biệt cắt ba mặt phẳng song song \(\left( P \right)\)
Đề bài
Cho \(a\), \(b\) là hai đường thẳng phân biệt cắt ba mặt phẳng song song \(\left( P \right)\), \(\left( Q \right)\), \(\left( R \right)\) lần lượt tại \(A,{\rm{ }}B,{\rm{ }}C\) và \(A',{\rm{ }}B',{\rm{ }}C'\). Khẳng định nào sau đây là SAI?
A. \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\)
B. \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{C'A'}}{{CA}}\)
C. \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\)
D. \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} = \frac{{AC}}{{A'C'}}\)
Phương pháp giải - Xem chi tiết
Sử dụng định lí Thales.
Lời giải chi tiết
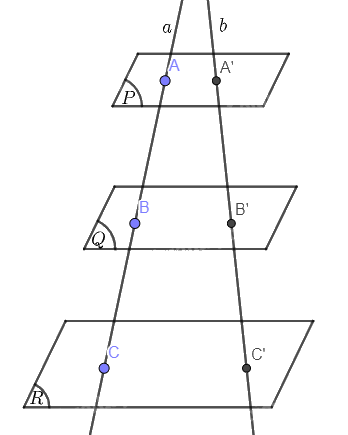
Áp dụng định lí Thales, ta có \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\). Như vậy, đáp án A đúng. Tương tự đáp án B cũng đúng.
Do \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} \Rightarrow \frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\), suy ra đáp án C đúng.
Đáp án D sai vì \(\frac{{AB}}{{BC}} \ne \frac{{AC}}{{A'C'}}\).
Vậy đáp án cần chọn là đáp án D.
Giải bài 32 trang 108 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải
Bài 32 trang 108 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về Đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về:
- Vecto chỉ phương và vecto pháp tuyến của đường thẳng và mặt phẳng.
- Phương trình đường thẳng và mặt phẳng.
- Quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng.
- Khoảng cách từ một điểm đến mặt phẳng.
Nội dung chi tiết bài 32 trang 108 SBT Toán 11 Cánh Diều
Để giải quyết bài 32 trang 108 SBT Toán 11 Cánh Diều một cách hiệu quả, bạn cần nắm vững các bước sau:
- Đọc kỹ đề bài: Xác định rõ các yếu tố đã cho và yêu cầu của bài toán.
- Xác định các đối tượng hình học: Xác định đường thẳng, mặt phẳng, điểm và các mối quan hệ giữa chúng.
- Sử dụng các công thức và định lý: Áp dụng các công thức và định lý liên quan đến vecto, phương trình đường thẳng, phương trình mặt phẳng và quan hệ giữa chúng.
- Kiểm tra lại kết quả: Đảm bảo kết quả của bạn phù hợp với điều kiện của bài toán và có ý nghĩa hình học hợp lý.
Lời giải chi tiết bài 32 trang 108 SBT Toán 11 Cánh Diều
(Ở đây sẽ là lời giải chi tiết cho từng ý của bài 32. Ví dụ:)
Ví dụ: Bài 32a
Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z = 5. Chứng minh rằng đường thẳng d song song với mặt phẳng (P).
Lời giải:
Vecto chỉ phương của đường thẳng d là a = (1, -1, 2). Vecto pháp tuyến của mặt phẳng (P) là n = (2, -1, 1).
Ta có a.n = 1*2 + (-1)*(-1) + 2*1 = 2 + 1 + 2 = 5 ≠ 0. Do đó, đường thẳng d không vuông góc với mặt phẳng (P).
Tuy nhiên, nếu bài toán yêu cầu chứng minh d song song với (P), cần kiểm tra thêm điều kiện: d không nằm trong (P). Chọn một điểm thuộc d, ví dụ A(1, 2, 3). Thay tọa độ A vào phương trình (P): 2*1 - 2 + 3 = 3 ≠ 5. Vậy A không thuộc (P), suy ra d song song với (P).
Mẹo giải nhanh và lưu ý quan trọng
- Nắm vững các công thức tính tích vô hướng của hai vecto.
- Sử dụng phương pháp tọa độ để giải quyết các bài toán về đường thẳng và mặt phẳng.
- Chú ý đến các trường hợp đặc biệt như đường thẳng song song, vuông góc với mặt phẳng, đường thẳng nằm trong mặt phẳng.
- Kiểm tra lại kết quả bằng cách thay các giá trị vào phương trình và so sánh với điều kiện của bài toán.
Tusach.vn - Đồng hành cùng bạn học Toán 11
Tusach.vn là website cung cấp lời giải bài tập Toán 11, Toán 12 và các môn học khác một cách nhanh chóng, chính xác và dễ hiểu. Chúng tôi hy vọng sẽ giúp các em học sinh học tập tốt hơn và đạt kết quả cao trong các kỳ thi.
Hãy truy cập Tusach.vn để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác!