Giải bài 58 trang 119 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 58 trang 119 sách bài tập Toán 11 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 58 trang 119 SBT Toán 11 Cánh Diều. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và nắm vững kiến thức liên quan đến nội dung bài học.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải chi tiết, giúp các em tự tin làm bài tập và đạt kết quả tốt nhất.
Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
Đề bài
Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
(1): Trong không gian, hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau,
(2): Trong không gian, hai đường thẳng vuông góc với nhau thì cùng nằm trên một mặt phẳng.
(3): Đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
(4): Đường thẳng song song với một trong hai mặt phẳng vuông góc thì song song hoặc nằm trên mặt phẳng còn lại.
(5): Ba mặt phẳng đôi một vuông góc với nhau thì ba giao tuyến tạo thành cũng đôi một vuông góc với nhau.
A. 2
B. 3
C. 4
D. 5
Phương pháp giải - Xem chi tiết
Xác định các mệnh đề là đúng hay sai.
Lời giải chi tiết
Khẳng định 1 là sai. Xét hình lập phương \(ABCD.A'B'C'D'\). Ta có \(AD\) và \(A'B'\) cùng vuông góc với \(AA'\), nhưng \(AD\) và \(A'B'\) không cùng nằm trong mặt phẳng nào cả.
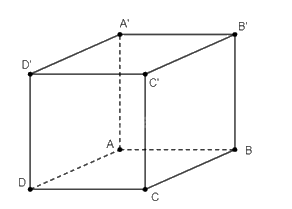
Khẳng định 2 là sai. Xét hình lập phương \(ABCD.A'B'C'D'\), ta thấy rằng \(BB'\) vuông góc với \(CD\), nhưng \(BB'\) và \(CD\) không cùng nằm trong mặt phẳng nào cả.
Khẳng định 3 là đúng, do theo tính chất, đường thẳng vuông góc với mặt phẳng thì nó sẽ vuông góc với tất cả các đường thẳng nằm trong mặt phẳng đó.
Khẳng định 4 là sai. Xét hình lập phương \(ABCD.A'B'C'D'\), ta thấy rằng hai mặt phẳng \(\left( {ABCD} \right)\) và \(\left( {BCC'B'} \right)\) vuông góc với nhau, đường thẳng \(A'B'\) song song với \(\left( {ABCD} \right)\), nhưng \(A'B'\) không song song hay nằm trong mặt phẳng \(\left( {BCC'B'} \right)\).
Khẳng định 5 là đúng. Xét ba mặt phẳng \(\left( P \right)\), \(\left( Q \right)\) và \(\left( R \right)\) đôi một vuông góc với nhau. Gọi \(a\), \(b\), \(c\) lần lượt là giao tuyến của các cặp mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\), \(\left( Q \right)\) và \(\left( R \right)\), \(\left( R \right)\) và \(\left( P \right)\).
Do \(\left( P \right)\) và \(\left( Q \right)\) cùng vuông góc với \(\left( R \right)\), nên giao tuyến \(a\) của \(\left( P \right)\) và \(\left( Q \right)\) cũng vuông góc với \(\left( R \right)\). Mà \(b\) và \(c\) cũng nằm trên \(\left( R \right)\) nên \(a\) vuông góc với \(b\) và \(a\) vuông góc với \(c\). Tương tự ta cũng suy ra \(b\) vuông góc với \(c\), tức là \(a\), \(b\), \(c\) đôi một vuông góc với nhau.
Đáp án đúng là A.
Giải bài 58 trang 119 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải
Bài 58 trang 119 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Nội dung chi tiết bài 58 trang 119 SBT Toán 11 Cánh Diều
Bài 58 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tính đạo hàm của hàm số.
- Dạng 2: Tìm cực trị của hàm số.
- Dạng 3: Khảo sát sự biến thiên của hàm số.
- Dạng 4: Ứng dụng đạo hàm để giải các bài toán tối ưu.
Lời giải chi tiết bài 58 trang 119 SBT Toán 11 Cánh Diều
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 58 trang 119 SBT Toán 11 Cánh Diều, chúng tôi xin trình bày lời giải chi tiết cho từng dạng bài tập:
Ví dụ 1: Tính đạo hàm của hàm số y = x3 - 2x2 + 5x - 1
Giải:
Áp dụng quy tắc tính đạo hàm, ta có:
y' = 3x2 - 4x + 5
Ví dụ 2: Tìm cực trị của hàm số y = x3 - 3x2 + 2
Giải:
- Tính đạo hàm bậc nhất: y' = 3x2 - 6x
- Tìm điểm dừng: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2
- Tính đạo hàm bậc hai: y'' = 6x - 6
- Xác định cực trị:
- Tại x = 0, y'' = -6 < 0, hàm số đạt cực đại tại x = 0, ymax = 2
- Tại x = 2, y'' = 6 > 0, hàm số đạt cực tiểu tại x = 2, ymin = -2
Mẹo giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, các em cần:
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra lại kết quả.
- Tham khảo các tài liệu tham khảo, sách giáo khoa, và các trang web học tập uy tín.
Tại sao nên chọn tusach.vn để giải bài tập Toán 11?
Tusach.vn là một trang web học tập uy tín, cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập Toán 11. Chúng tôi có đội ngũ giáo viên giàu kinh nghiệm, luôn cập nhật kiến thức mới nhất và phương pháp giải bài tập hiệu quả nhất. Ngoài ra, chúng tôi còn cung cấp nhiều tài liệu tham khảo hữu ích, giúp các em học sinh học tập tốt hơn.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và giải quyết các bài tập Toán 11 một cách dễ dàng!
| Dạng bài | Phương pháp giải |
|---|---|
| Tính đạo hàm | Áp dụng quy tắc tính đạo hàm |
| Tìm cực trị | Giải phương trình đạo hàm bằng 0, xét dấu đạo hàm bậc hai |