Giải bài 13 trang 94 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 13 trang 94 SBT Toán 11 Cánh Diều
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 13 trang 94 sách bài tập Toán 11 Cánh Diều. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, vì vậy chúng tôi đã biên soạn hướng dẫn này để giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Bài viết này sẽ cung cấp đáp án, phương pháp giải và những lưu ý quan trọng để bạn có thể hoàn thành bài tập một cách hiệu quả nhất.
Cho hình chóp S.ABCD có ABCD là hình bình hành và SA=SC, SB = SD.
Đề bài
Cho hình chóp S.ABCD có ABCD là hình bình hành và SA=SC, SB = SD. Gọi O là giao điểm của AC và BD. Chứng minh rằng \(SO \bot \left( {ABCD} \right).\)
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Lời giải chi tiết
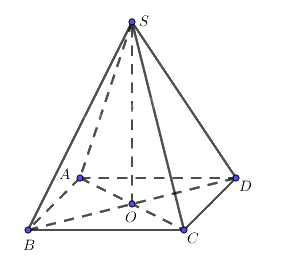
Vì ABCD là hình bình hành nên O là trung điểm của AC và BD.
Xét tam giác SAC cân tại S có SO là đường trung tuyến nên SO là đường cao\( \Rightarrow SO \bot AC.\)
Xét tam giác SBD cân tại S có SO là đường trung tuyến nên SO là đường cao, \( \Rightarrow SO \bot BD.\)
Mà AC, BD cắt nhau trong mặt phẳng (ABCD). Do đó \(SO \bot \left( {ABCD} \right).\)
Giải bài 13 trang 94 SBT Toán 11 Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Bài 13 trang 94 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, và các phép toán trên hàm số (tổng, hiệu, tích, thương).
Nội dung chính của bài 13 trang 94 SBT Toán 11 Cánh Diều
- Câu a: Tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 5
- Câu b: Tính đạo hàm của hàm số g(x) = sin(x) + cos(x)
- Câu c: Tính đạo hàm của hàm số h(x) = (x2 + 1) / (x - 1)
- Câu d: Tính đạo hàm của hàm số k(x) = x * ex
Hướng dẫn giải chi tiết từng câu
Câu a: f(x) = x3 - 3x2 + 2x - 5
Để tính đạo hàm của f(x), ta sử dụng quy tắc đạo hàm của tổng và quy tắc đạo hàm của lũy thừa:
- Đạo hàm của xn là n*xn-1
- Đạo hàm của hằng số là 0
Áp dụng các quy tắc trên, ta có:
f'(x) = 3x2 - 6x + 2
Câu b: g(x) = sin(x) + cos(x)
Để tính đạo hàm của g(x), ta sử dụng quy tắc đạo hàm của tổng và đạo hàm của các hàm lượng giác:
- Đạo hàm của sin(x) là cos(x)
- Đạo hàm của cos(x) là -sin(x)
Áp dụng các quy tắc trên, ta có:
g'(x) = cos(x) - sin(x)
Câu c: h(x) = (x2 + 1) / (x - 1)
Để tính đạo hàm của h(x), ta sử dụng quy tắc đạo hàm của thương:
(u/v)' = (u'v - uv') / v2
Trong đó: u = x2 + 1 và v = x - 1
Ta có: u' = 2x và v' = 1
Áp dụng quy tắc đạo hàm của thương, ta có:
h'(x) = ((2x)(x - 1) - (x2 + 1)(1)) / (x - 1)2 = (2x2 - 2x - x2 - 1) / (x - 1)2 = (x2 - 2x - 1) / (x - 1)2
Câu d: k(x) = x * ex
Để tính đạo hàm của k(x), ta sử dụng quy tắc đạo hàm của tích:
(uv)' = u'v + uv'
Trong đó: u = x và v = ex
Ta có: u' = 1 và v' = ex
Áp dụng quy tắc đạo hàm của tích, ta có:
k'(x) = (1)(ex) + (x)(ex) = ex + xex = ex(1 + x)
Lưu ý khi giải bài tập về đạo hàm
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Áp dụng đúng quy tắc khi tính đạo hàm của các hàm số phức tạp.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
- Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.
Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về cách giải bài 13 trang 94 sách bài tập Toán 11 Cánh Diều. Chúc bạn học tập tốt!
Tìm kiếm thêm: Tusach.vn cung cấp đầy đủ đáp án và lời giải các bài tập Toán 11 Cánh Diều.