Giải bài 44 trang 113 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 44 trang 113 SBT Toán 11 Cánh Diều
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 44 trang 113 sách bài tập Toán 11 Cánh Diều. Bài viết này sẽ giúp bạn hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu và cập nhật nhanh chóng nhất để hỗ trợ quá trình học tập của bạn.
Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh.
Đề bài
Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh.
Phương pháp giải - Xem chi tiết
Trước hết, cần chứng minh kết quả phụ: Trong một hình bình hành, tổng bình phương của hai đường chéo bằng tổng bình phương tất cả các cạnh của hình bình hành. Áp dụng kết quả này vào hình hộp.
Lời giải chi tiết
Trước hết, ta sẽ chứng minh kết quả phụ: Trong một hình bình hành, tổng bình phương của hai đường chéo bằng tổng bình phương tất cả các cạnh của hình bình hành. Xét hình bình hành \(MNPQ\) như hình dưới đây. Ta cần chứng minh rằng \(M{P^2} + N{Q^2} = M{N^2} + N{P^2} + P{Q^2} + Q{M^2}\)
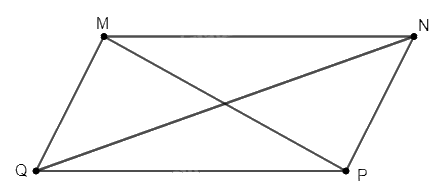
Áp dụng định lí cosin trong tam giác \(MPQ\) và \(NPQ\), ta có:
\(M{P^2} = Q{M^2} + Q{P^2} - 2QM.QP.\cos MQP\)
\(Q{N^2} = P{Q^2} + P{N^2} - 2PN.PQ.\cos QPN\).
Do \(QM = PN\) và \(\cos MQP = - \cos QPN\) (do \(\widehat {MQP}\) và \(\widehat {QPN}\) bù nhau), nên ta có
\(M{P^2} + N{Q^2} = M{Q^2} + 2P{Q^2} + P{N^2} - 2QM.QP\cos MQP + 2QM.QP\cos MQP\)
\( \Rightarrow M{P^2} + N{Q^2} = 2\left( {M{N^2} + N{P^2}} \right)\).
Ta có điều phải chứng minh.
Quay trở lại bài toán, ta xét hình hộp \(ABCD.A'B'C'D'\).
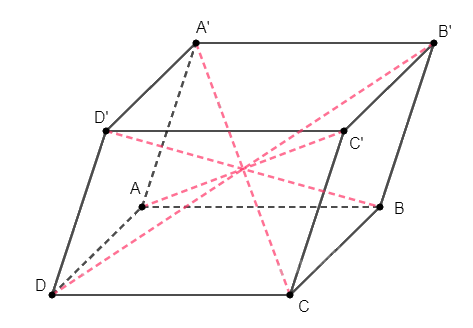
Áp dụng kết quả vừa chứng minh được ở trên với hai hình bình hành \(ACC'A'\), \(DBB'D'\) và \(A'B'C'D'\) ta có:
\(AC{'^2} + A'{C^2} = 2\left( {AA{'^2} + A'C{'^2}} \right)\) ; \(B'{D^2} + BD{'^2} = 2\left( {BB{'^2} + B'D{'^2}} \right)\);
\(A'C{'^2} + B'D{'^2} = 2\left( {A'B{'^2} + A'D{'^2}} \right)\).
Như vậy
\(AC{'^2} + A'{C^2} + BD{'^2} + B'{D^2} = 2\left( {AA{'^2} + A'C{'^2} + BB{'^2} + B'D{'^2}} \right)\)
\( = 4AA{'^2} + 2\left( {A'C{'^2} + B'D{'^2}} \right) = 4AA{'^2} + 4A'B{'^2} + 4A'D{'^2}\).
Do \(4AA{'^2} = AA{'^2} + BB{'^2} + CC{'^2} + DD{'^2}\), \(4A'B{'^2} = A'B{'^2} + A{B^2} + C'D{'^2} + C{D^2}\), \(4A'D{'^2} = A'D{'^2} + A{D^2} + B'C{'^2} + B{C^2}\), ta kết luận rằng trong một hình hộp, tổng bình phương tất cả các đường chéo bằng tổng tất cả các cạnh của hình hộp đó.
Bài toán được chứng minh.
Giải bài 44 trang 113 SBT Toán 11 Cánh Diều: Tổng quan
Bài 44 trang 113 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về Đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit và các phép toán trên hàm số (tổng, hiệu, tích, thương, hàm hợp).
Nội dung chi tiết bài 44 trang 113 SBT Toán 11 Cánh Diều
Bài 44 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của một hàm số cho trước.
- Tìm đạo hàm cấp hai: Yêu cầu tính đạo hàm cấp hai của một hàm số.
- Ứng dụng đạo hàm để giải phương trình: Sử dụng đạo hàm để tìm nghiệm của phương trình.
- Khảo sát hàm số: Sử dụng đạo hàm để xác định khoảng đồng biến, nghịch biến, cực trị của hàm số.
Hướng dẫn giải chi tiết bài 44 trang 113 SBT Toán 11 Cánh Diều
Để giải bài 44 trang 113 SBT Toán 11 Cánh Diều hiệu quả, bạn cần nắm vững các kiến thức sau:
- Các quy tắc tính đạo hàm cơ bản: Đạo hàm của hàm số lũy thừa, hàm lượng giác, hàm mũ, hàm logarit.
- Các quy tắc tính đạo hàm của phép toán trên hàm số: Quy tắc cộng, trừ, nhân, chia, hàm hợp.
- Các công thức đạo hàm đặc biệt: Đạo hàm của hàm số ẩn, đạo hàm của hàm số tham số.
Dưới đây là ví dụ minh họa cách giải một dạng bài tập thường gặp trong bài 44:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1
Giải:
Áp dụng quy tắc đạo hàm của hàm đa thức, ta có:
f'(x) = 3x2 + 4x - 5
Lưu ý khi giải bài 44 trang 113 SBT Toán 11 Cánh Diều
- Đọc kỹ đề bài để xác định đúng yêu cầu của bài toán.
- Sử dụng đúng các quy tắc và công thức đạo hàm.
- Kiểm tra lại kết quả sau khi tính toán.
- Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.
Tusach.vn – Hỗ trợ học tập Toán 11 hiệu quả
Tusach.vn cung cấp đầy đủ lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách bài tập Toán 11 Cánh Diều. Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Bảng tổng hợp các công thức đạo hàm thường dùng
| Hàm số | Đạo hàm |
|---|---|
| y = c (c là hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |
Chúc bạn học tập tốt và đạt kết quả cao!