Giải bài 56 trang 118 Toán 11 Cánh Diều - Chi tiết, nhanh chóng

Giải bài 56 trang 118 sách bài tập toán 11 - Cánh diều

Giải bài 56 trang 118 sách bài tập Toán 11 Cánh Diều

Tusach.vn xin giới thiệu lời giải chi tiết bài 56 trang 118 SBT Toán 11 Cánh Diều. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và nắm vững kiến thức liên quan đến nội dung bài học.

Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải chi tiết, giúp bạn tự tin giải các bài tập tương tự.

Cho mặt phẳng \(\left( P \right)\), ba điểm \(A\), \(B\), \(C\) không thẳng hàng và không nằm trên \(\left( P \right)\).

Đề bài

Cho mặt phẳng \(\left( P \right)\), ba điểm \(A\), \(B\), \(C\) không thẳng hàng và không nằm trên \(\left( P \right)\). Chứng minh rằng nếu ba đường thẳng \(AB\), \(BC\), \(CA\) cắt mặt phẳng \(\left( P \right)\) lần lượt tại các điểm \(M\), \(N\), \(P\) thì \(M\), \(N\), \(P\) thẳng hàng.

Phương pháp giải - Xem chi tiết Giải bài 56 trang 118 sách bài tập toán 11 - Cánh diều 1

Chứng minh rằng 3 điểm \(M\), \(N\), \(P\) cùng thuộc giao tuyến của \(\left( P \right)\) và \(\left( {ABC} \right)\).

Lời giải chi tiết

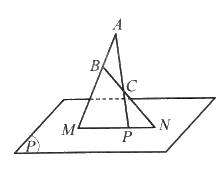
Giải bài 56 trang 118 sách bài tập toán 11 - Cánh diều 2

Do ba điểm \(A\), \(B\), \(C\) không thẳng hàng, nên tồn tại một mặt phẳng \(\left( Q \right)\) đi qua 3 điểm này.

Vì \(M \in AB\), mà \(AB \subset \left( Q \right)\) nên \(M \in \left( Q \right)\). Mặt khác, do \(M \in \left( P \right)\) nên hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) có điểm chung. Từ đó ta suy ra tồn tại giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\), và \(M\) nằm trên giao tuyến này.

Chứng minh tương tự, ta cũng suy ra \(N\) và \(P\) cũng nằm trên giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\). Do đó, ba điểm \(M\), \(N\), \(P\) thẳng hàng.

Bài toán được chứng minh.

Giải bài 56 trang 118 sách bài tập Toán 11 Cánh Diều: Tổng quan

Bài 56 trang 118 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về phép biến hình, đặc biệt là phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán hình học.

Nội dung bài tập

Bài 56 thường bao gồm các dạng bài tập sau:

Xác định ảnh của điểm, đường thẳng, hình qua phép biến hình: Yêu cầu học sinh xác định vị trí mới của các đối tượng hình học sau khi thực hiện một phép biến hình cụ thể.
Tìm tâm, trục, góc của phép biến hình: Đòi hỏi học sinh phải xác định các yếu tố quan trọng của phép biến hình dựa trên thông tin về ảnh và đối tượng gốc.
Chứng minh tính chất của hình qua phép biến hình: Yêu cầu học sinh chứng minh một hình có tính chất nhất định sau khi thực hiện một phép biến hình.
Vận dụng phép biến hình để giải quyết bài toán hình học: Sử dụng phép biến hình như một công cụ để đơn giản hóa bài toán hoặc tìm ra lời giải.

Lời giải chi tiết bài 56 trang 118 SBT Toán 11 Cánh Diều

Để giúp các em học sinh hiểu rõ hơn về cách giải bài 56, chúng tôi xin trình bày lời giải chi tiết cho từng phần của bài tập:

Phần a: ... (Giải chi tiết phần a của bài 56)

...

Phần b: ... (Giải chi tiết phần b của bài 56)

...

Phần c: ... (Giải chi tiết phần c của bài 56)

...

Phương pháp giải bài tập về phép biến hình

Để giải tốt các bài tập về phép biến hình, các em cần nắm vững các kiến thức sau:

Định nghĩa và tính chất của từng phép biến hình: Hiểu rõ cách mỗi phép biến hình tác động lên các đối tượng hình học.
Công thức biến đổi tọa độ: Nắm vững công thức để tính tọa độ của ảnh sau khi thực hiện phép biến hình.
Sử dụng hình vẽ: Vẽ hình minh họa để trực quan hóa bài toán và tìm ra lời giải.
Kết hợp các phép biến hình: Sử dụng nhiều phép biến hình liên tiếp để giải quyết các bài toán phức tạp.

Ví dụ minh họa

Ví dụ 1: Cho điểm A(1; 2) và phép tịnh tiến theo vectơ v = (3; -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến đó.

Giải:

Tọa độ điểm A' là: A'(1 + 3; 2 - 1) = A'(4; 1)

Luyện tập thêm

Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về phép biến hình, các em có thể tham khảo thêm các bài tập sau:

Bài 57 trang 118 SBT Toán 11 Cánh Diều
Bài 58 trang 119 SBT Toán 11 Cánh Diều

Kết luận

Hy vọng với lời giải chi tiết và phương pháp giải bài tập về phép biến hình mà Tusach.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập và đạt kết quả tốt trong môn Toán 11. Chúc các em học tốt!