Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I\), \(J\),\(K\), \(L\) lần lượt là trọng tâm của các tam giác \(SAB\), \(SBC\), \(SCD\), \(SAD\).
a) Chứng minh rằng bốn điểm \(I\), \(J\),\(K\), \(L\) đồng phẳng và tứ giác \(IJKL\) là hình bình hành.
b) Chứng minh rằng \(JL\parallel {\rm{CD}}\).
c) Xác định giao tuyến của hai mặt phẳng \(\left( {IJKL} \right)\) và \(\left( {SCD} \right)\).
Phương pháp giải - Xem chi tiết
a) Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(BC\), \(CD\), \(DA\).
Chứng minh rằng \(MNPQ\) là hình bình hành. Chứng minh rằng \(IJ\parallel LK\) và \(IJ = LK\), để suy ra tứ giác \(IJLK\) là hình bình hành.
b) Chứng minh \(JL\) và \(CD\) cùng song song với \(NQ\), từ đó suy ra \(JL\parallel CD\).
c) Từ kết quả câu b, và sử dụng tính chất “Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó, hoặc trùng với một trong hai đường thẳng đó” để tìm giao tuyến của hai mặt phẳng \(\left( {IJKL} \right)\) và \(\left( {SCD} \right)\).
Lời giải chi tiết
a) Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(BC\), \(CD\), \(DA\).
Ta có \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(BC\), nên \(MN\) là đường trung bình của tam giác \(ABC\). Suy ra \(MN\parallel AC\) và \(MN = \frac{1}{2}AC\).
Tương tự ta có \(PQ\parallel AC\) và \(PQ = \frac{1}{2}AC\).
Suy ra \(MN\parallel PQ\) và \(MN = PQ\). Vậy tứ giác \(MNPQ\) là hình bình hành.
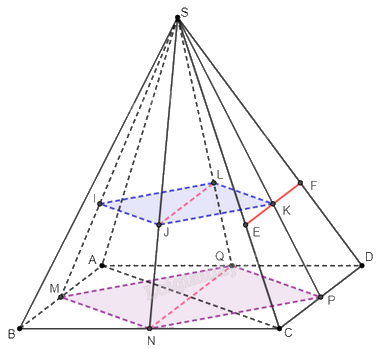
Ta có \(I\) là trọng tâm của tam giác \(SAB\), nên suy ra \(I \in SM\) và \(\frac{{SI}}{{SM}} = \frac{2}{3}\).
Chứng minh tương tự ta cũng có \(J \in SN\) và \(\frac{{SJ}}{{SN}} = \frac{2}{3}\).
Tam giác \(SMN\) có \(\frac{{SI}}{{SM}} = \frac{{SJ}}{{SN}} = \frac{2}{3}\), theo hệ quả của định lí Thales ta suy ra \(IJ\parallel MN\) và \(\frac{{IJ}}{{MN}} = \frac{2}{3}\).
Chứng minh tương tự ta cũng có \(LK\parallel PQ\) và \(\frac{{LK}}{{PQ}} = \frac{2}{3}\).
Từ đó ta suy ra \(IJ\parallel LK\) và \(IJ = LK\). Vậy bốn điểm \(I\), \(J\), \(K\), \(L\) đồng phẳng và tứ giác \(IJLK\) là hình bình hành.
b) Ta có \(L\) là trọng tâm của tam giác \(SAD\), nên suy ra \(L \in SQ\) và \(\frac{{SL}}{{SQ}} = \frac{2}{3}\).
Suy ra \(\frac{{SL}}{{SQ}} = \frac{{SJ}}{{SN}}\), tức là \(JL\parallel NQ\).
Mặt khác \(N\) là trung điểm của \(BC\),\(Q\) là trung điểm của \(DA\) nên suy ra \(NQ\parallel CD\).
Vậy \(JL\parallel CD\).
c) Xét hai mặt phẳng \(\left( {IJKL} \right)\)và \(\left( {SCD} \right)\), ta có \(JL\parallel CD\), \(JL \in \left( {IJKL} \right)\), \(CD \in \left( {SCD} \right)\).
Hơn nữa \(K \in \left( {IJKL} \right) \cap \left( {SCD} \right)\) và \(K \notin JL\), \(K \notin CD\)
Xét hai mặt phẳng \(\left( {IJKL} \right)\)và \(\left( {SCD} \right)\), ta có \(K \in \left( {IJKL} \right) \cap \left( {SCD} \right)\), tức là \(K\) nằm trên giao tuyến của hai mặt phẳng đó. Hơn nữa, \(K \notin JL\), \(K \notin CD\), nên \(JL\) và \(CD\) không là giao tuyến của hai mặt phẳng trên.
Mặt khác, ta có \(JL\parallel CD\), \(JL \in \left( {IJKL} \right)\), \(CD \in \left( {SCD} \right)\) nên giao tuyến của \(\left( {IJKL} \right)\)và \(\left( {SCD} \right)\) là một đường thẳng đi qua \(K\) và song song với \(CD\). Trên hình vẽ, giao tuyến của chúng là đường thẳng \(EF\) đi qua \(K\) và song song với \(CD\).
