Giải bài 16 trang 95 SBT Toán 11 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 16 trang 95 sách bài tập Toán 11 Cánh Diều. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những nội dung chất lượng nhất để hỗ trợ học sinh trong quá trình học tập.
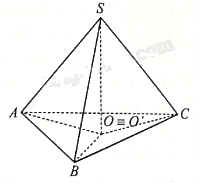
Cho hình chóp S.ABC thoả mãn SA = SB = SC.
Giải bài 16 trang 95 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải
Bài 16 trang 95 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng để giải quyết các bài toán thực tế.
Nội dung chi tiết bài 16 trang 95 SBT Toán 11 Cánh Diều
Bài 16 bao gồm các dạng bài tập sau:
- Dạng 1: Xác định mối quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng.
- Dạng 2: Tính góc giữa đường thẳng và mặt phẳng.
- Dạng 3: Tìm điều kiện để đường thẳng vuông góc với mặt phẳng.
- Dạng 4: Bài toán ứng dụng thực tế liên quan đến đường thẳng và mặt phẳng.
Lời giải chi tiết bài 16 trang 95 SBT Toán 11 Cánh Diều
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 16:
Câu 1: (Trích dẫn câu hỏi từ SBT)
(Ví dụ: Cho hình chóp S.ABCD có đáy là hình vuông ABCD. Gọi M là trung điểm của CD. Chứng minh rằng AM vuông góc với BM.)
Lời giải:
- Xét tam giác MCD, M là trung điểm của CD nên DM = MC.
- Áp dụng định lý Pitago vào tam giác ADM, ta có: AM2 = AD2 + DM2.
- Áp dụng định lý Pitago vào tam giác BCM, ta có: BM2 = BC2 + MC2.
- Vì ABCD là hình vuông nên AD = BC. Suy ra AM2 = BM2.
- Do đó, AM = BM.
- Xét tam giác ABM, AM = BM nên tam giác ABM cân tại M.
- Gọi H là trung điểm của AB. Khi đó MH vuông góc với AB.
- Vì AM = BM nên MH là đường trung tuyến đồng thời là đường cao của tam giác ABM.
- Suy ra AM vuông góc với BM. (đpcm)
Câu 2: (Trích dẫn câu hỏi từ SBT)
(Ví dụ: Tính góc giữa đường thẳng SA và mặt phẳng (ABCD) trong hình chóp S.ABCD.)
Lời giải:
Để tính góc giữa đường thẳng SA và mặt phẳng (ABCD), ta thực hiện các bước sau:
- Kẻ AH vuông góc với BD tại H.
- Kẻ SK vuông góc với AH tại K.
- Khi đó, góc SAH là góc giữa đường thẳng SA và mặt phẳng (ABCD).
- Tính AH, SK và sử dụng các hàm lượng giác để tính góc SAH.
Mẹo giải bài tập về đường thẳng và mặt phẳng
Để giải tốt các bài tập về đường thẳng và mặt phẳng, bạn nên:
- Nắm vững các định lý, tính chất về quan hệ song song, vuông góc.
- Vẽ hình minh họa chính xác.
- Sử dụng các công cụ hình học để hỗ trợ giải toán.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Tusach.vn – Nơi đồng hành cùng bạn học Toán 11
Tusach.vn luôn cập nhật lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong sách bài tập Toán 11 Cánh Diều. Hãy truy cập Tusach.vn để học Toán 11 hiệu quả và đạt kết quả cao!
Chúc các bạn học tốt!