Giải bài 50 trang 110 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 50 trang 110 SBT Toán 11 Cánh Diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 50 trang 110 sách bài tập Toán 11 Cánh Diều. Bài giải này được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp những nội dung chất lượng nhất để hỗ trợ học sinh trong quá trình học tập.
Cho hình hộp \(ABCD.A'B'C'D'\) có \(ABCD\) là hình thoi cạnh \(a\)
Đề bài
Cho hình hộp \(ABCD.A'B'C'D'\) có \(ABCD\) là hình thoi cạnh \(a\), \(AA' \bot \left( {ABCD} \right)\), \(AA' = 2a\), \(AC = a\). Tính khoảng cách:
a) Từ điểm \(A\) đến mặt phẳng \(\left( {BCC'B'} \right)\).
b) Giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {CDD'C'} \right)\).
c*) Giữa hai đường thẳng \(BD\) và \(A'C\).
Phương pháp giải - Xem chi tiết
a) Gọi \(H\) là trung điểm của cạnh \(BC\). Ta chứng minh \(H\) là hình chiếu của \(A\) trên mặt phẳng \(\left( {BCC'B'} \right)\), từ đó khoảng cách cần tìm là đoạn thẳng \(AH\).
b) Gọi \(I\) là trung điểm của cạnh \(DC\). Do \(\left( {ABB'A'} \right)\parallel \left( {DCC'D'} \right)\), nên khoảng cách giữa hai mặt phẳng này là khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {DCC'D'} \right)\). Ta chứng minh \(I\) là hình chiếu của \(A\) trên mặt phẳng \(\left( {DCC'D'} \right)\), từ đó khoảng cách cần tìm là đoạn thẳng \(AI\).
c) Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Gọi \(E\) là hình chiếu của \(O\) trên \(A'C\). Ta chứng minh \(OE\) là đường vuông góc chung của 2 đường thẳng \(BD\) và \(A'C\), từ đó khoảng cách cần tính là đoạn thẳng \(OE\).
Lời giải chi tiết
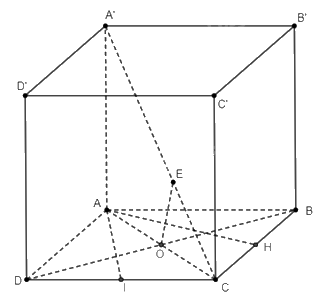
a) Gọi \(H\) là trung điểm của cạnh \(BC\). Tam giác \(ABC\) đều (\(AB = BC = AC = a\)) nên ta suy ra \(AH \bot BC\).
Do \(BB' \bot \left( {ABCD} \right)\), ta suy ra \(BB' \bot AH\).
Như vậy, do \(AH \bot BC\), \(BB' \bot AH\) nên \(AH \bot \left( {BCC'B'} \right)\), điều này có nghĩa \(H\) là hình chiếu của \(A\) trên mặt phẳng \(\left( {BCC'B'} \right)\). Vậy khoảng cách từ \(A\) đến \(\left( {BCC'B'} \right)\) là đoạn thẳng \(AH\).
Tam giác \(ABC\) đều cạnh \(a\), đường cao \(AH\) nên \(AH = \frac{{a\sqrt 3 }}{2}\).
Vậy khoảng cách từ \(A\) đến \(\left( {BCC'B'} \right)\) là \(\frac{{a\sqrt 3 }}{2}\).
b) Do \(ABCD.A'B'C'D'\) là hình hộp, nên \(\left( {ABB'A'} \right)\parallel \left( {DCC'D'} \right)\). Suy ra khoảng cách giữa hai mặt phẳng này cũng bằng khoảng cách từ \(A\) đến mặt phẳng \(\left( {DCC'D'} \right)\).
Gọi \(I\) là trung điểm của cạnh \(DC\). Tam giác \(ADC\) có \(AB = DC = AC = a\) nên nó là tam giác đều. Suy ra \(AI \bot DC\) và \(AI = \frac{{a\sqrt 3 }}{2}\).
Do \(DD' \bot \left( {ABCD} \right)\), ta suy ra \(DD' \bot AI\). Như vậy, do \(AI \bot DC\), \(DD' \bot AI\) nên \(AI \bot \left( {DCC'D'} \right)\). Điều này có nghĩa \(I\) là hình chiếu của \(A\) trên mặt phẳng \(\left( {DCC'D'} \right)\). Vậy khoảng cách giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {DCC'D'} \right)\), bằng khoảng cách từ \(A\) trên mặt phẳng \(\left( {DCC'D'} \right)\), là đoạn thẳng \(AI\), và bằng \(\frac{{a\sqrt 3 }}{2}\).
c) Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Do \(ABCD\) là hình thoi nên \(AC \bot BD\) và \(AO = \frac{{AC}}{2} = \frac{a}{2}\)
Do \(AA' \bot \left( {ABCD} \right)\), nên \(AA' \bot BD\). Như vậy, do \(AC \bot BD\), \(AA' \bot BD\) nên \(\left( {AA'C} \right) \bot BD\).
Gọi \(E\) là hình chiếu của \(O\) trên \(A'C\). Vì \(OE \subset \left( {AA'C} \right)\), \(\left( {AA'C} \right) \bot BD\) nên \(OE \bot BD\). Như vậy \(OE\) là đường vuông góc chung của 2 đường thẳng \(BD\) và \(A'C\), điều này có nghĩa khoảng cách giữa \(BD\) và \(A'C\) là đoạn thẳng \(OE\).
Tam giác \(CEO\) và \(CAA'\) có chung góc \(C\) và có góc vuông \(\widehat {CEO} = \widehat {CAA'}\) nên chúng đồng dạng với nhau. Suy ra \(\frac{{OE}}{{AA'}} = \frac{{CO}}{{CA'}} \Rightarrow OE = \frac{{AA'.CO}}{{CA'}}\)
Tam giác \(AA'C\) vuông tại \(A\), nên \(A'C = \sqrt {A'{A^2} + A{C^2}} = \sqrt {{{\left( {2a} \right)}^2} + {a^2}} = a\sqrt 5 \).
Do đó \(OE = \frac{{AA'.OC}}{{A'C}} = \frac{{2a.\frac{a}{2}}}{{a\sqrt 5 }} = \frac{{a\sqrt 5 }}{5}\).
Giải bài 50 trang 110 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải
Bài 50 trang 110 sách bài tập Toán 11 Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của hàm số hợp, và các ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Nội dung chi tiết bài 50 trang 110 SBT Toán 11 Cánh Diều
Bài 50 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tính đạo hàm của hàm số.
- Dạng 2: Tìm cực trị của hàm số.
- Dạng 3: Khảo sát sự biến thiên của hàm số.
- Dạng 4: Ứng dụng đạo hàm để giải các bài toán tối ưu.
Lời giải chi tiết bài 50 trang 110 SBT Toán 11 Cánh Diều
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 50 trang 110 SBT Toán 11 Cánh Diều, Tusach.vn xin trình bày lời giải chi tiết cho từng câu hỏi:
Câu a: (Ví dụ minh họa)
Cho hàm số y = x3 - 3x2 + 2. Tính đạo hàm y' của hàm số.
Lời giải:
y' = 3x2 - 6x
Câu b: (Ví dụ minh họa)
Tìm cực trị của hàm số y = x3 - 3x2 + 2.
Lời giải:
- Tính đạo hàm y' = 3x2 - 6x.
- Giải phương trình y' = 0 để tìm các điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2.
- Tính đạo hàm bậc hai y'' = 6x - 6.
- Xét dấu y'' tại các điểm cực trị:
- y''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0. Giá trị cực đại là y(0) = 2.
- y''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là y(2) = -2.
Mẹo giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, các em học sinh cần:
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Đồng hành cùng học sinh trên con đường chinh phục Toán học
Tusach.vn là website chuyên cung cấp lời giải chi tiết các bài tập Toán từ lớp 6 đến lớp 12. Chúng tôi luôn cập nhật những nội dung mới nhất và chất lượng nhất để giúp các em học sinh học tập hiệu quả. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Công thức | Mô tả |
|---|---|
| (xn)' = nxn-1 | Đạo hàm của lũy thừa |
| (u + v)' = u' + v' | Đạo hàm của tổng |