Đề bài
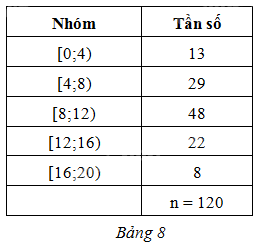
Cho mẫu số liệu ghép nhóm thống kê thời gian sử dụng điện thoại trước khi ngủ (đơn vị: phút) của một người trong 120 ngày như ở Bảng 8. Xác định các số đặc trưng đo xu thế trung tâm cho mẫu số liệu đó (làm tròn các kết quả đến hàng phần mười).
Phương pháp giải - Xem chi tiết
Áp dụng các công thức đã học để xác định các đại lượng tiêu biểu.
Lời giải chi tiết
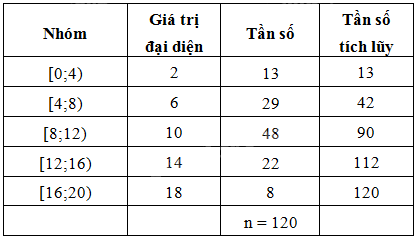
- Thời gian sử dụng điện thoại trung bình trước khi ngủ của một người trong 120 ngày là:
\(\bar x = \frac{{2.13 + 6.29 + 10.48 + 14.22 + 18.8}}{{120}} \approx 9,4\) (phút).
- Ta có: \(\frac{n}{2} = \frac{{120}}{2} = 60\) mà \(42 < 60 < 90.\) Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 60.
Xét nhóm 3 là nhóm [8;12) có \(r = 8,{\rm{ }}d = 4,{\rm{ }}{n_3} = 48\) và nhóm 2 là nhóm [4;8) có \(c{f_2} = 42.\)
Trung vị của mẫu số liệu là:
\({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 8 + \left( {\frac{{60 - 42}}{{48}}} \right).4 = 9,5\) (phút).
Tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = {M_e} = 9,5\) (phút).
- Ta có: \(\frac{n}{4} = \frac{{120}}{4} = 30\) mà \(13 < 30 < 42.\) Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 2 là nhóm [4;8) có \(s = 4,{\rm{ }}h = 4,{\rm{ }}{n_2} = 29\) và nhóm 1 là nhóm [0;4) có \(c{f_1} = 13.\)
Tứ phân vị thứ nhất của mẫu số liệu là:
\({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 4 + \left( {\frac{{30 - 13}}{{29}}} \right).4 \approx 6,3\) (phút).
- Ta có: \(\frac{{3n}}{4} = \frac{{3.120}}{4} = 90\) mà \(90 = 90 < 112.\) Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 90.
Xét nhóm 4 là nhóm [12;16) có \(t = 12,{\rm{ }}l = 2,{\rm{ }}{n_4} = 22\) và nhóm 3 là nhóm [8;12) có \(c{f_3} = 90.\)
Tứ phân vị thứ ba của mẫu số liệu là:
\({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l = 12 + \left( {\frac{{90 - 90}}{{22}}} \right).4 = 12\)(phút).
- Ta thấy: Nhóm 3 ứng với nửa khoảng [8;12) là nhóm có tần số lớn nhất với \(u = 8,{\rm{ }}g = 4,{\rm{ }}{n_3} = 48,{\rm{ }}{n_2} = 29,{\rm{ }}{n_4} = 22.\)
Mốt của mẫu số liệu là:
\({M_0} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 8 + \left( {\frac{{48 - 29}}{{2.48 - 29 - 22}}} \right).4 \approx 9,7\) (phút).


