Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 37 trang 112 sách bài tập toán 11 - Cánh diều
SBT Toán 11 - Cánh diều
SBT TOÁN TẬP 1 - CÁNH DIỀU
Chương IV. Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài 5. Hình lăng trụ và hình hộp

Giải bài 37 trang 112 sách bài tập toán 11 - Cánh diều

Giải bài 37 trang 112 SBT Toán 11 Cánh Diều

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 37 trang 112 sách bài tập Toán 11 Cánh Diều. Bài viết này sẽ giúp bạn hiểu rõ phương pháp giải và tự tin làm bài tập.

Chúng tôi luôn cố gắng cung cấp nội dung chất lượng cao, dễ hiểu và phù hợp với chương trình học Toán 11 hiện hành.

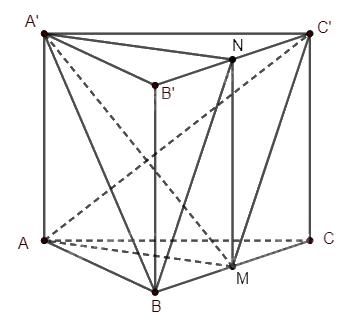
Cho hình lăng trụ tam giác \(ABC.A'B'C'\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(BC\), \(B'C'\).

Đề bài

Cho hình lăng trụ tam giác \(ABC.A'B'C'\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(BC\), \(B'C'\). Khẳng định nào sau đây là đúng?

A. \(\left( {A'MN} \right)\parallel \left( {ACC'} \right)\)

B. \(\left( {A'BN} \right)\parallel \left( {AC'M} \right)\)

C. \(C'M\parallel \left( {A'B'B} \right)\)

D. \(BN\parallel \left( {ACC'A'} \right)\)

Phương pháp giải - Xem chi tiếtGiải bài 37 trang 112 sách bài tập toán 11 - Cánh diều 1

Sử dụng các tính chất về đường thẳng song song với mặt phẳng, các tính chất về hai mặt phẳng song song.

Lời giải chi tiết

Giải bài 37 trang 112 sách bài tập toán 11 - Cánh diều 2

Ta nhận xét rằng \(A' \in \left( {A'MN} \right)\) và \(A' \in \left( {ACC'A'} \right)\), nên hai mặt phẳng \(\left( {A'MN} \right)\) và \(\left( {ACC'} \right)\) có điểm chung, tức là chúng không song song với nhau.

Xét hai mặt phẳng \(\left( {A'BN} \right)\) và \(\left( {AC'M} \right)\). Do \(M\) và \(N\) lần lượt là trung điểm của \(BC\) và \(B'C'\), nên ta có \(BM = C'N = \frac{1}{2}BC\). Hơn nữa, do \(BC\parallel B'C'\) nên tứ giác \(BMC'N\) là hình bình hành. Suy ra \(BN\parallel C'M\), mà do \(C'M \subset \left( {AC'M} \right)\) nên \(BN\parallel \left( {AC'M} \right)\).

Mặt khác, vì \(M\) và \(N\) lần lượt là trung điểm của \(BC\) và \(B'C'\) nên \(MN\parallel BB'\) và \(MN = BB'\). Do \(ABC.A'B'C'\) là lăng trụ tam giác, nên \(BB'\parallel AA'\) và \(BB' = AA'\). Từ đó ta có \(MN = AA'\) và \(MN\parallel AA'\). Điều này có nghĩa tứ giác \(A'NMA\) là hình bình hành. Suy ra \(A'N\parallel AM\). Do \(AM \subset \left( {AC'M} \right)\) nên \(A'N\parallel \left( {AC'M} \right)\). Vậy \(\left( {A'BN} \right)\parallel \left( {AC'M} \right)\).

Xét mặt phẳng \(\left( {BCC'B'} \right)\), ta thấy rằng \(BB'\) và \(CM\) cắt nhau, mà do \(BB' \subset \left( {A'B'B} \right)\) nên \(CM\) và \(\left( {A'B'B} \right)\) có điểm chung, tức là chúng không song song với nhau.

Chứng minh tương tự, ta cũng suy ra \(BN\) và \(\left( {ACC'A'} \right)\) không song song với nhau.

Đáp án đúng là B.

Giải bài 37 trang 112 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải

Bài 37 trang 112 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về Đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.

Nội dung chính của bài 37 trang 112 SBT Toán 11 Cánh Diều

Bài 37 thường bao gồm các dạng bài tập sau:

  • Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của các hàm số đơn thức, đa thức, và các hàm số phức tạp hơn.
  • Áp dụng quy tắc tính đạo hàm: Vận dụng các quy tắc như quy tắc cộng, trừ, nhân, chia, quy tắc hàm hợp để tính đạo hàm.
  • Giải phương trình đạo hàm: Tìm nghiệm của phương trình đạo hàm để xác định các điểm cực trị, điểm uốn của hàm số.
  • Ứng dụng đạo hàm để giải quyết các bài toán thực tế: Ví dụ như tìm vận tốc, gia tốc, hoặc tối ưu hóa các đại lượng.

Lời giải chi tiết bài 37 trang 112 SBT Toán 11 Cánh Diều

Để giúp bạn hiểu rõ hơn, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài 37. Lưu ý rằng, việc nắm vững các khái niệm và quy tắc đạo hàm là rất quan trọng để giải quyết bài tập này.

Ví dụ minh họa (Giả định bài tập cụ thể):

Bài tập: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1

Lời giải:

  1. Áp dụng quy tắc đạo hàm của tổng: f'(x) = d/dx (3x2) + d/dx (2x) - d/dx (1)
  2. Áp dụng quy tắc đạo hàm của lũy thừa: d/dx (3x2) = 6x
  3. Áp dụng quy tắc đạo hàm của hàm số tuyến tính: d/dx (2x) = 2
  4. Đạo hàm của hằng số bằng 0: d/dx (1) = 0
  5. Kết hợp lại: f'(x) = 6x + 2

Mẹo giải bài tập đạo hàm hiệu quả

  • Nắm vững các quy tắc đạo hàm: Đây là nền tảng để giải quyết mọi bài tập về đạo hàm.
  • Phân tích kỹ đề bài: Xác định rõ hàm số cần tính đạo hàm và các yêu cầu của bài toán.
  • Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi có chức năng tính đạo hàm có thể giúp bạn kiểm tra lại kết quả.
  • Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp bạn làm quen với các dạng bài và rèn luyện kỹ năng giải quyết vấn đề.

Tài liệu tham khảo hữu ích

Ngoài sách bài tập, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 11:

  • Sách giáo khoa Toán 11
  • Các trang web học Toán trực tuyến
  • Các video bài giảng về đạo hàm

Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về bài 37 trang 112 sách bài tập Toán 11 Cánh Diều. Chúc bạn học tập tốt!

Bảng tổng hợp các quy tắc đạo hàm cơ bản

Quy tắcCông thức
Đạo hàm của hằng sốd/dx (c) = 0
Đạo hàm của hàm số lũy thừad/dx (xn) = nxn-1
Đạo hàm của hàm số tuyến tínhd/dx (cx) = c

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN