Đề bài
Cho hình chóp \(S.ABCD\) đáy là hình bình hành. Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của \(SB\), \(BC\), \(CD\).
a) Chứng minh rằng \(SC\parallel \left( {MNP} \right)\).
b) Xác định giao tuyến của mặt phẳng \(\left( {MNP} \right)\) với mặt phẳng \(\left( {SCD} \right)\) và giao điểm \(Q\) của đường thẳng \(SD\) với mặt phẳng \(\left( {MNP} \right)\).
c) Xác định giao điểm \(E\) của đường thẳng \(SA\) với mặt phẳng \(\left( {MNP} \right)\).
d) Tính tỉ số \(\frac{{SE}}{{SA}}\).
Phương pháp giải - Xem chi tiết
a) Để chứng minh \(SC\parallel \left( {MNP} \right)\), ta cần chứng minh rằng \(SC\) song song với một đường thẳng nằm trong \(\left( {MNP} \right)\).
b) Gọi \(Q\) là trung điểm của \(SD\). Chứng minh rằng \(Q \in \left( {MNP} \right)\), từ đó suy ra \(PQ\) là giao tuyến của \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\), từ đó ta cũng chứng minh được \(Q\) là giao điểm của \(SD\) và \(\left( {MNP} \right)\).
c) Gọi \(I\) là giao điểm của \(NP\) và \(AC\). Trên cạnh \(SA\) lấy \(E\) sao cho \(IE\parallel SC\). Chứng minh rằng \(E \in \left( {MNP} \right)\) và suy ra \(E\) là giao điểm cần tìm.
d) Sử dụng định lí Thales để tính tỉ số \(\frac{{SE}}{{SA}}\).
Lời giải chi tiết
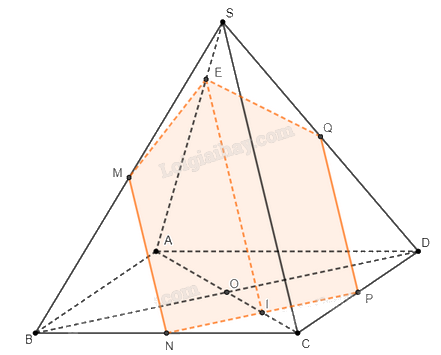
a) Do \(M\) là trung điểm của \(SB\), \(N\) là trung điểm của \(BC\) nên \(MN\) là đường trung bình của tam giác \(SBC\). Suy ra \(MN\parallel SC\).
Vì \(MN \subset \left( {MNP} \right)\) nên \(SC\parallel \left( {MNP} \right)\). Ta có điều phải chứng minh.
b) Gọi \(Q\) là trung điểm của \(SD\). Ta sẽ chứng minh \(PQ\) chính là giao tuyến của \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\), và \(Q\) cũng chính là giao điểm của \(SD\) và \(\left( {MNP} \right)\).
Thật vậy, xét hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\), ta có \(P \in CD \subset \left( {SCD} \right)\) và \(P \in \left( {MNP} \right)\), nên giao tuyến của \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\) là một đường thẳng đi qua \(P\).
Hơn nữa, do \(MN\parallel SC\), \(SC \subset \left( {SCD} \right)\), \(MN \subset \left( {MNP} \right)\), ta suy ra giao tuyến của \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\) là một đường thẳng đi qua \(P\) và song song với \(SC\).
Vì \(P\) là trung điểm của \(CD\), \(Q\) là trung điểm của \(SD\) nên \(PQ\) là đường trung bình của tam giác \(SDC\). Suy ra \(PQ\parallel SC\) và \(PQ\parallel MN\). Do \(PQ\parallel MN\) nên \(Q \in \left( {MNP} \right)\).
Như vậy, \(PQ\) chính là giao tuyến của \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\).
Do \(Q \in \left( {MNP} \right)\) và \(Q \in SD\), ta suy ra \(Q\) là giao điểm của \(SD\) và \(\left( {MNP} \right)\).
c) Gọi \(I\) là giao điểm của \(NP\) và \(AC\). Trên cạnh \(SA\) lấy \(E\) sao cho \(IE\parallel SC\).
Dễ thấy rằng do \(I \in NP\), \(NP \subset \left( {MNP} \right)\) nên \(I \in \left( {MNP} \right)\).
Do \(IE\parallel SC\), \(MN\parallel SC\) , ta suy ra \(IE\parallel MN\). Vì \(I \in \left( {MNP} \right)\), ta suy ra \(E \in \left( {MNP} \right)\).
Như vậy \(E\) là điểm chung của \(SA\) và \(\left( {MNP} \right)\), ta kết luận \(E\) chính là giao điểm của \(SA\) và \(\left( {MNP} \right)\).
d) Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Ta có \(P\) là trung điểm của \(CD\), \(N\) là trung điểm của \(BC\) nên \(NP\) là đường trung bình của tam giác \(BCD\). Suy ra \(NP\parallel BD\), hay \(NI\parallel BO\). Do \(N\) là trung điểm của \(BC\), ta kết luận rằng \(I\) là trung điểm của \(OC\), hay \(\frac{{CI}}{{CO}} = \frac{1}{2}\).
Mặt khác, do \(ABCD\) là hình bình hành, \(O\) là giao điểm của \(AC\) và \(BD\), ta suy ra \(O\) là trung điểm của \(AC\), hay \(\frac{{CO}}{{CA}} = \frac{1}{2}\).
Suy ra \(\frac{{CI}}{{CA}} = \frac{{CI}}{{CO}}.\frac{{CO}}{{CA}} = \frac{1}{2}.\frac{1}{2} = \frac{1}{4}\).
Tam giác \(SAC\) có \(IE\parallel SC\), theo định lí Thales ta có \(\frac{{CI}}{{IA}} = \frac{{SE}}{{EA}} \Rightarrow \frac{{CI}}{{CA}} = \frac{{SE}}{{SA}}\).
Như vậy \(\frac{{SE}}{{SA}} = \frac{1}{4}\).
