Đề bài
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Tính:
a) Khoảng cách giữa hai mặt phẳng \(\left( {ABCD} \right)\) và \(\left( {A'B'C'D'} \right)\).
b) Số đo của góc nhị diện \(\left[ {A,CD,B'} \right]\).
c) Tang của góc giữa đường thẳng \(BD'\) và mặt phẳng \(\left( {ABCD} \right)\).
d) Khoảng cách giữa hai đường thẳng \(C'D\) và \(BC\).
e*) Góc giữa hai đường thẳng \(BC'\) và \(CD'\).
Phương pháp giải - Xem chi tiết
a) Ta sẽ chỉ ra \(AA'\) chính là khoảng cách giữa hai mặt phẳng \(\left( {ABCD} \right)\) và \(\left( {A'B'C'D'} \right)\).
b) Ta chứng minh \(\widehat {ADA'}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,CD,B'} \right]\).
c) Ta chứng minh \(\widehat {DBD'}\) là góc tạo bởi đường thẳng \(BD'\) và mặt phẳng \(\left( {ABCD} \right)\). Do đó, ta cần tính \(\tan \widehat {DBD'}\).
d) Gọi \(I\) là giao điểm của \(DC'\) và \(D'C\). Chứng minh rằng \(IC\) là đường vuông góc chung của hai đường thẳng \(BC\) và \(DC'\), từ đó khoảng cách cần tính là đoạn thẳng \(IC\).
e*) Chỉ ra rằng do \(AD'\parallel BC'\) nên góc giữa \(BC'\) và \(CD'\) băng góc giữa \(AD'\) và \(CD'\), và bằng góc \(\widehat {AD'C}\).
Lời giải chi tiết
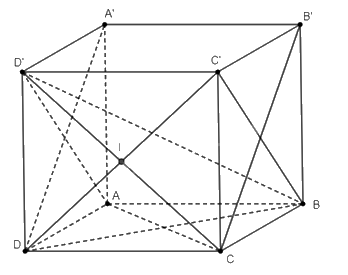
a) Do \(ABCD.A'B'C'D'\) là hình lập phương, nên ta có \(AA' \bot \left( {ABCD} \right)\), \(AA' \bot \left( {A'B'C'D'} \right)\) và \(\left( {ABCD} \right)\parallel \left( {A'B'C'D'} \right)\). Do đó khoảng cách giữa hai mặt phẳng \(\left( {ABCD} \right)\) và \(\left( {A'B'C'D'} \right)\) cũng bằng khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {A'B'C'D'} \right)\), và bằng \(AA'\).
Do \(ABCD.A'B'C'D'\) là hình lập phương cạnh \(a\), nên ta có \(AA' = a\).
Vậy khoảng cách giữa hai mặt phẳng \(\left( {ABCD} \right)\) và \(\left( {A'B'C'D'} \right)\) bằng \(a\).
b) Do \(ABCD.A'B'C'D'\) là hình lập phương, nên ta có \(AD \bot CD\), \(CD \bot \left( {DAA'D'} \right)\) và \(ADD'A'\) là hình vuông.
Ta nhận xét rằng \(A'D\parallel B'C\), và \(CD \bot A'D\) (do \(CD \bot \left( {DAA'D'} \right)\)), cùng với \(AD \bot CD\), ta suy ra \(\widehat {ADA'}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,CD,B'} \right]\).
Vì \(ADD'A'\) là hình vuông nên \(\widehat {ADA'} = {45^o}\).
Vậy số đo của góc nhị diện \(\left[ {A,CD,B'} \right]\) bằng \({45^o}\).
c) Do \(D\) là hình chiếu của \(D'\) trên \(\left( {ABCD} \right)\), nên \(\widehat {DBD'}\) là góc tạo bởi đường thẳng \(BD'\) và mặt phẳng \(\left( {ABCD} \right)\).
Do \(ABCD\) là hình vuông cạnh \(a\), nên ta có \(BD = a\sqrt 2 \).
Ta có \(\tan \widehat {DBD'} = \frac{{DD'}}{{BD}} = \frac{a}{{a\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) (tam giác \(DBD'\) vuông tại \(D\))
Vậy tang của góc tạo bởi đường thẳng \(BD'\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(\frac{{\sqrt 2 }}{2}\).
d) Gọi \(I\) là giao điểm của \(DC'\) và \(D'C\). Do \(ABCD.A'B'C'D'\) là hình lập phương, nên \(DCC'D'\) là hình vuông, suy ra \(IC \bot DC'\).
Mặt khác, cũng do \(ABCD.A'B'C'D'\) là hình lập phương, ta suy ra \(BC \bot \left( {DCC'D'} \right)\), điều này dẫn tới \(IC \bot BC\).
Như vậy, ta có \(IC\) là đường vuông góc chung của hai đường thẳng \(BC\) và \(DC'\), tức khoảng cách giữa \(BC\) và \(DC'\) là đoạn thẳng \(IC\).
Do \(DCC'D'\) là hình vuông cạnh \(a\), nên \(D'C = a\sqrt 2 \Rightarrow IC = \frac{{a\sqrt 2 }}{2}\).
Vậy khoảng cách giữa \(BC\) và \(DC'\) là \(\frac{{a\sqrt 2 }}{2}\).
e*) Do \(AD'\parallel BC'\) nên góc giữa \(BC'\) và \(CD'\) băng góc giữa \(AD'\) và \(CD'\), tức là góc \(\widehat {AD'C}\).
Tam giác \(AD'C\) có \(AD' = D'C = AC\) (do đều là mỗi đường chéo của các mặt trong hình lập phương) nên tam giác \(AD'C\) đều. Suy ra \(\widehat {AD'C} = {60^o}\).
Vậy góc giữa \(BC'\) và \(CD'\) bằng \({60^o}\).
