Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 53 trang 117 sách bài tập toán 11 - Cánh diều
SBT Toán 11 - Cánh diều
SBT TOÁN TẬP 1 - CÁNH DIỀU
Chương IV. Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài 6. Phép chiếu song song. Hình biểu diễn của một hình không gian

Giải bài 53 trang 117 sách bài tập toán 11 - Cánh diều

Giải bài 53 trang 117 SBT Toán 11 Cánh Diều

Tusach.vn xin giới thiệu lời giải chi tiết bài 53 trang 117 sách bài tập Toán 11 Cánh Diều. Bài giải này được xây dựng dựa trên kiến thức đã học trong chương trình, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và nhanh chóng nhất để hỗ trợ học sinh trong quá trình học tập.

Cho hình chóp (S.ABCD) có đáy là hình bình hành. Trên cạnh (SA) lấy điểm (M)

Đề bài

Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Trên cạnh \(SA\) lấy điểm \(M\) sao cho \(MA = 2MS\). Mặt phẳng \(\left( {CDM} \right)\) cắt \(SB\) tại \(N\). Tỉ số \(\frac{{SN}}{{SB}}\) bằng:

A. \(\frac{1}{2}\)

B. \(\frac{1}{3}\)

C. \(\frac{2}{3}\)

D. \(\frac{3}{4}\)

Phương pháp giải - Xem chi tiếtGiải bài 53 trang 117 sách bài tập toán 11 - Cánh diều 1

Chứng minh rằng \(MN\) là giao tuyến của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\), từ đó suy ra \(MN\parallel AB\) và tính tỉ số \(\frac{{SN}}{{SB}}\).

Lời giải chi tiết

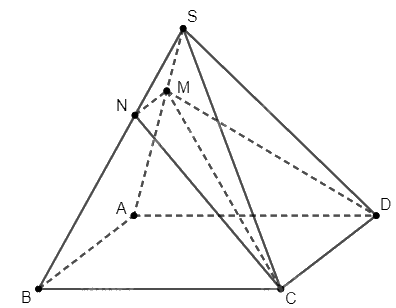
Giải bài 53 trang 117 sách bài tập toán 11 - Cánh diều 2

Ta thấy rằng \(M \in \left( {CDM} \right) \cap \left( {SAB} \right)\) và \(N\) là giao điểm của \(\left( {CDM} \right)\) và \(SB\). Do \(SB \subset \left( {SAB} \right)\) nên \(N\) là điểm chung của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\). Từ đó ta suy ra \(MN\) là giao tuyến của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\).

Nhận xét rằng \(AB\parallel CD\), \(AB \subset \left( {SAB} \right)\), \(CD \subset \left( {CDM} \right)\), \(MN\) là giao tuyến của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\), ta suy ra \(MN\parallel AB\).

Theo định lí Thales, ta có \(\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}}\). Do \(MA = 2MS \Rightarrow \frac{{SM}}{{SA}} = \frac{1}{3}\).

Như vậy \(\frac{{SN}}{{SB}} = \frac{1}{3}\). Đáp án đúng là B.

Giải bài 53 trang 117 SBT Toán 11 Cánh Diều: Tổng quan và Phương pháp giải

Bài 53 trang 117 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về Đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.

Nội dung chính của bài 53 trang 117 SBT Toán 11 Cánh Diều

Bài 53 thường bao gồm các dạng bài tập sau:

  • Tính đạo hàm của hàm số tại một điểm.
  • Tìm đạo hàm của hàm số.
  • Ứng dụng đạo hàm để giải các bài toán liên quan đến cực trị, khoảng đơn điệu của hàm số.
  • Giải các bài toán thực tế liên quan đến đạo hàm.

Lời giải chi tiết bài 53 trang 117 SBT Toán 11 Cánh Diều

Để giải bài 53 trang 117 SBT Toán 11 Cánh Diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:

  1. Khái niệm đạo hàm: Hiểu rõ định nghĩa đạo hàm của hàm số tại một điểm và đạo hàm của hàm số.
  2. Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản (hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit) và các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
  3. Ứng dụng của đạo hàm: Biết cách sử dụng đạo hàm để tìm cực trị, khoảng đơn điệu của hàm số và giải các bài toán thực tế.

Dưới đây là lời giải chi tiết cho từng phần của bài 53 (ví dụ, giả sử bài 53 có 3 câu):

Câu a: Tính đạo hàm của hàm số f(x) = x2 + 2x - 1 tại x = 1

Lời giải:

f'(x) = 2x + 2

f'(1) = 2(1) + 2 = 4

Vậy, đạo hàm của hàm số f(x) tại x = 1 là 4.

Câu b: Tìm đạo hàm của hàm số g(x) = sin(x) + cos(x)

Lời giải:

g'(x) = cos(x) - sin(x)

Vậy, đạo hàm của hàm số g(x) là cos(x) - sin(x).

Câu c: Tìm khoảng đơn điệu của hàm số h(x) = x3 - 3x2 + 2

Lời giải:

h'(x) = 3x2 - 6x

Giải phương trình h'(x) = 0, ta được x = 0 và x = 2.

Xét dấu h'(x) trên các khoảng (-∞; 0), (0; 2), (2; +∞), ta thấy:

  • Trên khoảng (-∞; 0), h'(x) > 0, hàm số h(x) đồng biến.
  • Trên khoảng (0; 2), h'(x) < 0, hàm số h(x) nghịch biến.
  • Trên khoảng (2; +∞), h'(x) > 0, hàm số h(x) đồng biến.

Vậy, hàm số h(x) đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).

Mẹo giải bài tập về đạo hàm

Để giải các bài tập về đạo hàm một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:

  • Nắm vững các quy tắc tính đạo hàm cơ bản.
  • Sử dụng bảng đạo hàm để tra cứu nhanh chóng.
  • Phân tích kỹ đề bài để xác định đúng dạng bài tập và phương pháp giải phù hợp.
  • Kiểm tra lại kết quả sau khi giải xong.

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử.

Tusach.vn hy vọng với lời giải chi tiết và những hướng dẫn trên, bạn sẽ tự tin hơn khi giải bài 53 trang 117 SBT Toán 11 Cánh Diều và đạt kết quả tốt trong môn Toán.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN