Giải bài 22 trang 95 sách bài tập toán 11 - Cánh diều
Tổng quan nội dung
Giải bài 22 trang 95 SBT Toán 11 Cánh Diều
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 22 trang 95 sách bài tập Toán 11 Cánh Diều. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, vì vậy chúng tôi đã biên soạn hướng dẫn này để giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Bài viết này sẽ cung cấp đáp án, phương pháp giải và các lưu ý quan trọng để bạn có thể hoàn thành bài tập một cách hiệu quả nhất.
Cho mặt phẳng (P) và hai điểm A, B sao cho B thuộc (P) và 4 không thuộc (P).
Đề bài
Cho mặt phẳng (P) và hai điểm A, B sao cho B thuộc (P) và 4 không thuộc (P). Điểm C chuyển động trên mặt phẳng (P) thoả mãn \(\widehat {ACB} = {90^0}.\) Chứng minh rằng C chuyển động trên một đường tròn cố định trong (P).
Phương pháp giải - Xem chi tiết
Sử dụng định lý ba đường vuông góc.
Lời giải chi tiết
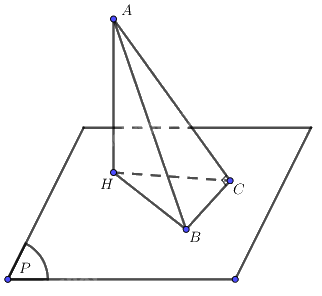
Gọi H là hình chiếu của A trên (P).
Khi đó H cố định và HC là hình chiếu của AC trên (P).
Vì \(BC \bot AC\) nên theo định lí ba đường vuông góc ta có \(BC \bot HC.\)
Do đó C chuyển động trên đường tròn đường kính HB cố định nằm trong (P).
Giải bài 22 trang 95 SBT Toán 11 Cánh Diều: Tổng quan và Hướng dẫn chi tiết
Bài 22 trang 95 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương và hàm hợp. Việc nắm vững các quy tắc này là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Nội dung chính của bài 22 trang 95 SBT Toán 11 Cánh Diều
- Phần 1: Tính đạo hàm của các hàm số đơn giản.
- Phần 2: Tính đạo hàm của hàm hợp.
- Phần 3: Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số.
Hướng dẫn giải chi tiết từng phần
Phần 1: Tính đạo hàm của các hàm số đơn giản
Để tính đạo hàm của các hàm số đơn giản, bạn cần áp dụng các quy tắc đạo hàm cơ bản như:
- Đạo hàm của hằng số bằng 0.
- Đạo hàm của xn bằng nxn-1.
- Đạo hàm của sin(x) bằng cos(x).
- Đạo hàm của cos(x) bằng -sin(x).
Ví dụ: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1.
Giải: f'(x) = 6x + 2.
Phần 2: Tính đạo hàm của hàm hợp
Để tính đạo hàm của hàm hợp, bạn cần áp dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x).
Ví dụ: Tính đạo hàm của hàm số f(x) = sin(x2).
Giải: f'(x) = cos(x2) * 2x = 2xcos(x2).
Phần 3: Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số
Để tìm phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm x0, bạn cần thực hiện các bước sau:
- Tính đạo hàm f'(x).
- Tính hệ số góc k = f'(x0).
- Tìm tọa độ điểm tiếp xúc (x0, f(x0)).
- Viết phương trình tiếp tuyến theo công thức: y - f(x0) = k(x - x0).
Ví dụ: Tìm phương trình tiếp tuyến của đồ thị hàm số y = x2 tại điểm x = 1.
Giải:
- f'(x) = 2x
- k = f'(1) = 2
- Điểm tiếp xúc: (1, 1)
- Phương trình tiếp tuyến: y - 1 = 2(x - 1) => y = 2x - 1
Lưu ý khi giải bài tập
- Nắm vững các quy tắc đạo hàm cơ bản.
- Áp dụng quy tắc đạo hàm của hàm hợp một cách chính xác.
- Kiểm tra lại kết quả sau khi tính toán.
- Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa và sách bài tập Toán 11. Chúng tôi hy vọng rằng với hướng dẫn này, bạn sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.