Lý thuyết Phương trình và bất phương trình mũ - SGK Toán 11 Cùng khám phá
Tổng quan nội dung
Lý thuyết Phương trình và Bất phương trình mũ - Toán 11
Chào mừng bạn đến với chuyên mục Lý thuyết Phương trình và Bất phương trình mũ dành cho học sinh lớp 11.
Chuyên mục này cung cấp đầy đủ kiến thức nền tảng, các định nghĩa, tính chất quan trọng và phương pháp giải các dạng bài tập thường gặp trong SGK Toán 11.
Tusach.vn cam kết mang đến cho bạn những bài học chất lượng, dễ hiểu và giúp bạn nắm vững kiến thức một cách nhanh chóng.
1. Phương trình mũ cơ bản Phương trình mũ cơ bản có dạng
A. Lý thuyết
1. Phương trình mũ cơ bản
Phương trình mũ cơ bản có dạng \({a^x} = b\) \((a > 0,a \ne 1)\).
Cho phương trình \({a^x} = b\) \((a > 0,a \ne 1)\): - Nếu b > 0 thì phương trình có nghiệm duy nhất \(x = {\log _a}b\). - Nếu \(b \le 0\) thì phương trình vô nghiệm. |
Lưu ý: Với a > 0 và \(a \ne 1\) và \(b = {a^\alpha }\) thì phương trình \({a^x} = b\) trở thành \({a^x} = {a^\alpha }\). Khi đó phương trình có nghiệm duy nhất \(x = \alpha \). Một cách tổng quát, với a > 0 và \(a \ne 1\) , ta có:
\({a^{A(x)}} = {a^{B(x)}} \Leftrightarrow A(x) = B(x)\).
2. Bất phương trình mũ cơ bản
Bất phương trình mũ cơ bản có dạng \({a^x} > b\) hoặc \({a^x} \ge b\), \({a^x} < b\), \({a^x} \le b\) \((a > 0,a \ne 1)\).
Cho bất phương trình \({a^x} > b\) \((a > 0,a \ne 1)\): - Nếu \(b \le 0\) thì bất phương trình nghiệm đúng với mọi \(x \in \mathbb{R}\). - Nếu b > 0 và: + a > 1: Ta có \({a^x} > b \Leftrightarrow x > {\log _a}b\). + 0 < a < 1: Ta có \({a^x} > b \Leftrightarrow x < {\log _a}b\). |
Lưu ý:
Giải tương tự cho các trường hợp còn lại: \({a^x} \ge b\), \({a^x} < b\), \({a^x} \le b\).
Với a > 0, \(a \ne 1\) và \(b = {a^\alpha }\) thì bất phương trình \({a^x} > b\) trở thành \({a^x} > {a^\alpha }\). Khi đó:
- Nếu a > 1 thì \({a^x} > {a^\alpha } \Leftrightarrow x > \alpha \).
- Nếu 0 < a < 1 thì \({a^x} > {a^\alpha } \Leftrightarrow x < \alpha \).
Một cách tổng quát, ta có:
- Khi a > 1 thì \({a^{A(x)}} > {a^{B(x)}} \Leftrightarrow A(x) > B(x)\).
- Khi 0 < a < 1 thì \({a^{A(x)}} > {a^{B(x)}} \Leftrightarrow A(x) < B(x)\).
B. Bài tập
Bài 1: Giải các phương trình:
a) \({3^{x + 1}} = \frac{1}{9}\).
b) \({2^{2x - 1}} + {4^{x + 1}} = 5\).
Giải:
a) \({3^{x + 1}} = \frac{1}{9} \Leftrightarrow x + 1 = {\log _3}\frac{1}{9} \Leftrightarrow x + 1 = - 2 \Leftrightarrow x = - 3\).
Vậy phương trình có nghiệm là x = -3.
b) \({2^{2x - 1}} + {4^{x + 1}} = 5 \Leftrightarrow \frac{1}{2}{.4^x} + {4.4^x} = 5 \Leftrightarrow \frac{9}{2}{.4^x} = 5 \Leftrightarrow {4^x} = \frac{{10}}{9} \Leftrightarrow x = {\log _4}\frac{{10}}{9}\).
Vậy phương trình có nghiệm là \(x = {\log _4}\frac{{10}}{9}\).
Bài 2: Giải các bất phương trình:
a) \({2^x} \ge \frac{1}{{32}}\).
b) \({\left( {\frac{1}{2}} \right)^{x + 1}} + {\left( {\frac{1}{2}} \right)^{x - 1}} > 15\).
Giải:
a) Vì cơ số 2 lớn hơn 1 nên \({2^x} \ge \frac{1}{{32}} \Leftrightarrow x \ge {\log _2}\frac{1}{{32}} \Leftrightarrow x \ge - 5\).
Vậy tập nghiệm của bất phương trình là \([ - 5; + \infty )\).
b) \({\left( {\frac{1}{2}} \right)^{x + 1}} + {\left( {\frac{1}{2}} \right)^{x - 1}} > 15 \Leftrightarrow \frac{1}{2}.{\left( {\frac{1}{2}} \right)^x} + 2.{\left( {\frac{1}{2}} \right)^x} > 15 \Leftrightarrow \frac{5}{2}.{\left( {\frac{1}{2}} \right)^x} > 15 \Leftrightarrow {\left( {\frac{1}{2}} \right)^x} > 6 \Leftrightarrow x < {\log _{\frac{1}{2}}}6\) (do cơ số \(\frac{1}{2} < 1\)).
Vậy tập nghiệm của bất phương trình là \(( - \infty ;{\log _{\frac{1}{2}}}6)\).
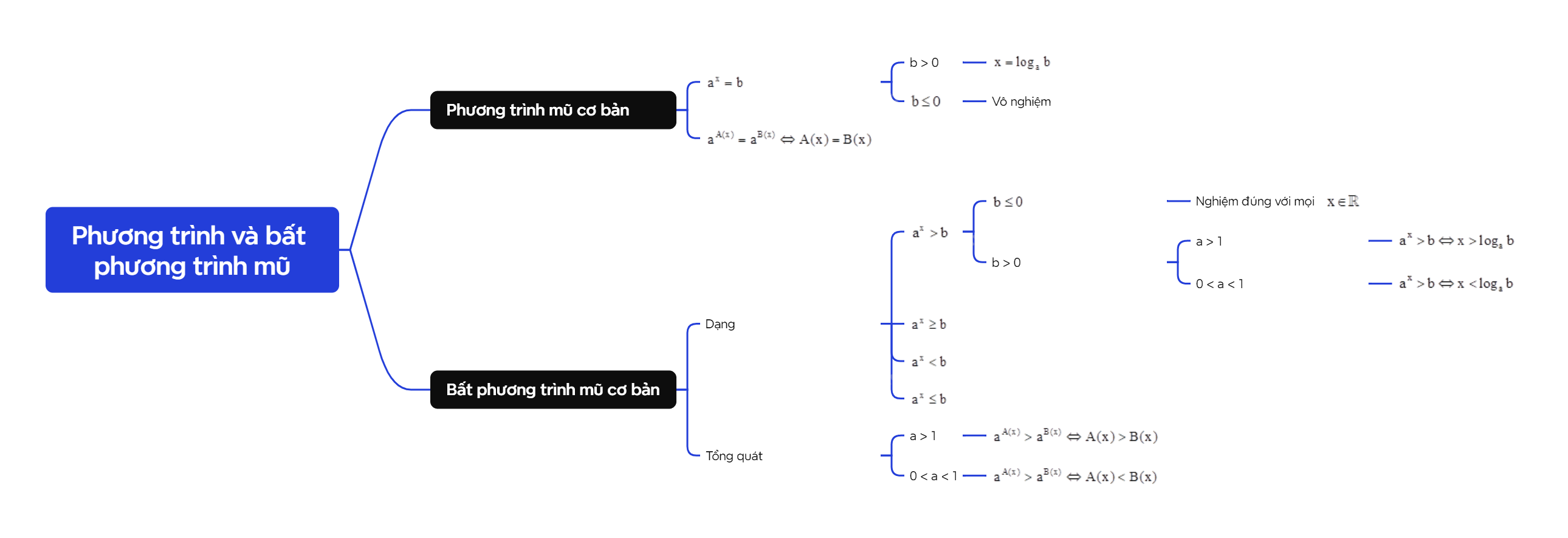
Lý Thuyết Phương Trình và Bất Phương Trình Mũ - SGK Toán 11: Tổng Quan và Phương Pháp Giải
Phương trình và bất phương trình mũ là một trong những chủ đề quan trọng trong chương trình Toán 11, thường xuất hiện trong các kỳ thi học kỳ, thi tốt nghiệp THPT và tuyển sinh Đại học. Việc nắm vững lý thuyết và phương pháp giải các bài toán này là điều cần thiết để đạt kết quả tốt môn Toán.
1. Khái Niệm Cơ Bản
Phương trình mũ: Là phương trình có chứa ẩn số trong số mũ. Ví dụ: 2x = 8.
Bất phương trình mũ: Là bất phương trình có chứa ẩn số trong số mũ. Ví dụ: 3x > 9.
Để giải phương trình và bất phương trình mũ, chúng ta cần nắm vững các tính chất của hàm số mũ và các phép biến đổi tương đương.
2. Các Tính Chất Quan Trọng của Hàm Số Mũ
- Hàm số mũ y = ax (với a > 0 và a ≠ 1) là hàm số đồng biến nếu a > 1 và nghịch biến nếu 0 < a < 1.
- Hàm số mũ luôn dương với mọi x.
- Đồ thị hàm số mũ luôn đi qua điểm (0, 1).
3. Phương Pháp Giải Phương Trình Mũ
Có nhiều phương pháp để giải phương trình mũ, tùy thuộc vào dạng phương trình cụ thể. Một số phương pháp phổ biến bao gồm:
- Đưa về cùng cơ số: Nếu có thể, hãy đưa cả hai vế của phương trình về cùng một cơ số. Ví dụ: 2x = 8 có thể viết thành 2x = 23, suy ra x = 3.
- Lấy logarit hai vế: Nếu không thể đưa về cùng cơ số, hãy lấy logarit hai vế của phương trình với cùng một cơ số.
- Đặt ẩn phụ: Trong một số trường hợp, việc đặt ẩn phụ có thể giúp đơn giản hóa phương trình.
4. Phương Pháp Giải Bất Phương Trình Mũ
Tương tự như phương trình mũ, có nhiều phương pháp để giải bất phương trình mũ. Một số phương pháp phổ biến bao gồm:
- Xét hàm số mũ: Sử dụng tính chất đơn điệu của hàm số mũ để so sánh các giá trị.
- Lấy logarit hai vế: Lưu ý rằng khi lấy logarit hai vế của một bất phương trình, cần phải đổi dấu bất phương trình nếu cơ số logarit nhỏ hơn 1.
5. Ví Dụ Minh Họa
Ví dụ 1: Giải phương trình 32x-1 = 27.
Giải:
32x-1 = 33
2x - 1 = 3
2x = 4
x = 2
Ví dụ 2: Giải bất phương trình 2x > 16.
Giải:
2x > 24
x > 4
6. Luyện Tập và Củng Cố Kiến Thức
Để nắm vững kiến thức về phương trình và bất phương trình mũ, bạn nên luyện tập thường xuyên với các bài tập trong SGK và các tài liệu tham khảo khác. Tusach.vn cung cấp một hệ thống bài tập đa dạng và phong phú, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
7. Tổng Kết
Hy vọng rằng chuyên mục Lý thuyết Phương trình và Bất phương trình mũ - Toán 11 trên tusach.vn sẽ giúp bạn học tập hiệu quả và đạt kết quả tốt trong môn Toán. Chúc bạn thành công!