Bài 9.14 Trang 102 SGK Toán 11 Tập 2

Bài 9.14 trang 102 SGK Toán 11 tập 2 - Cùng khám phá

Bài 9.14 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các công thức đạo hàm cơ bản và kỹ năng tính đạo hàm của hàm số.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Một quân vua được đặt trên một ô giữa bàn cờ vua. Mỗi bước di chuyển, quân vua được chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng (Hình 9,3).

Đề bài

Một quân vua được đặt trên một ô giữa bàn cờ vua. Mỗi bước di chuyển, quân vua được chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng (Hình 9,3). Bạn An di chuyển quân vua ngẫu nhiên 3 bước. Tính xác suất sau 3 bước quân vua trở về ô xuất phát.

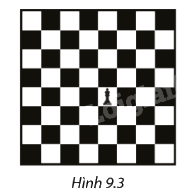
Bài 9.14 trang 102 SGK Toán 11 tập 2 - Cùng khám phá 1

Phương pháp giải - Xem chi tiết Bài 9.14 trang 102 SGK Toán 11 tập 2 - Cùng khám phá 2

Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng \( \Rightarrow n\left( \Omega \right)\)

Gọi A là biến cố: “Quân vua sau 3 bước trở về đúng vị trí ban đầu”. Tính \(n\left( A \right)\).

Lời giải chi tiết

Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng \(n\left( \Omega \right) = {8^3}\)

Gọi A là biến cố: “Quân vua sau 3 bước trở về đúng vị trí ban đầu”

TH1: Quân vua di chuyển bước thứ nhất sang ô đen liền kề (được tô màu đỏ) có 4

cách.

Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 4 cách.

Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.

Vậy TH này có 4.4 = 16 cách.

TH2: Quân vua di chuyển bước thứ nhất sang các ô trắng liền kề (được tô màu đỏ) có 4 cách.

Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 2 cách.

Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.

Vậy TH này có 4.2 = 8 cách

\(n\left( A \right) = 8.3 = 24 \Rightarrow P\left( A \right) = \frac{{24}}{{{8^3}}} = \frac{3}{{64}}\)

Bài 9.14 Trang 102 SGK Toán 11 Tập 2: Giải Chi Tiết và Hướng Dẫn

Bài 9.14 trang 102 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này, được trình bày một cách dễ hiểu và logic.

Nội dung bài tập:

Bài 9.14 yêu cầu học sinh tính đạo hàm của hàm số và sử dụng đạo hàm để giải quyết một bài toán liên quan đến vận tốc và gia tốc.

Lời giải chi tiết:

Để giải bài tập này, chúng ta cần thực hiện các bước sau:

Bước 1: Tính đạo hàm của hàm số. Sử dụng các công thức đạo hàm cơ bản để tính đạo hàm của hàm số đã cho.
Bước 2: Phân tích bài toán. Đọc kỹ đề bài và xác định các thông tin quan trọng, như vận tốc ban đầu, gia tốc, và thời gian.
Bước 3: Áp dụng đạo hàm để giải bài toán. Sử dụng đạo hàm để tìm vận tốc và gia tốc tại một thời điểm nhất định.
Bước 4: Kiểm tra kết quả. Đảm bảo rằng kết quả của bạn hợp lý và phù hợp với điều kiện của bài toán.

Ví dụ minh họa:

Giả sử hàm số biểu diễn vị trí của một vật chuyển động theo thời gian là s(t) = t³ - 3t² + 2t. Để tìm vận tốc của vật tại thời điểm t = 2, chúng ta cần tính đạo hàm của s(t) và thay t = 2 vào đạo hàm đó.

Đạo hàm của s(t) là v(t) = s'(t) = 3t² - 6t + 2. Thay t = 2 vào v(t), ta được v(2) = 3(2)² - 6(2) + 2 = 2. Vậy vận tốc của vật tại thời điểm t = 2 là 2 đơn vị.

Các lưu ý khi giải bài tập:

Nắm vững các công thức đạo hàm cơ bản.
Đọc kỹ đề bài và xác định đúng các thông tin cần thiết.
Sử dụng đạo hàm một cách chính xác và hợp lý.
Kiểm tra kết quả để đảm bảo tính chính xác.

Bài tập tương tự:

Để củng cố kiến thức, bạn có thể giải thêm các bài tập tương tự trong SGK Toán 11 tập 2 hoặc các tài liệu tham khảo khác.

Tóm tắt:

Bài 9.14 trang 102 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về đạo hàm và ứng dụng của nó. Bằng cách thực hiện các bước giải chi tiết và lưu ý các điểm quan trọng, bạn có thể tự tin giải quyết bài tập này và các bài tập tương tự.

Bảng tổng hợp công thức đạo hàm cơ bản:

Hàm số	Đạo hàm
y = c (hằng số)	y' = 0
y = xⁿ	y' = nx^n-1
y = sin x	y' = cos x
y = cos x	y' = -sin x

Hy vọng với lời giải chi tiết và hướng dẫn này, các bạn học sinh sẽ hiểu rõ hơn về Bài 9.14 trang 102 SGK Toán 11 tập 2 và đạt kết quả tốt trong môn học.