Lý thuyết Hai mặt phẳng song song - SGK Toán 11 Cùng khám phá
Tổng quan nội dung
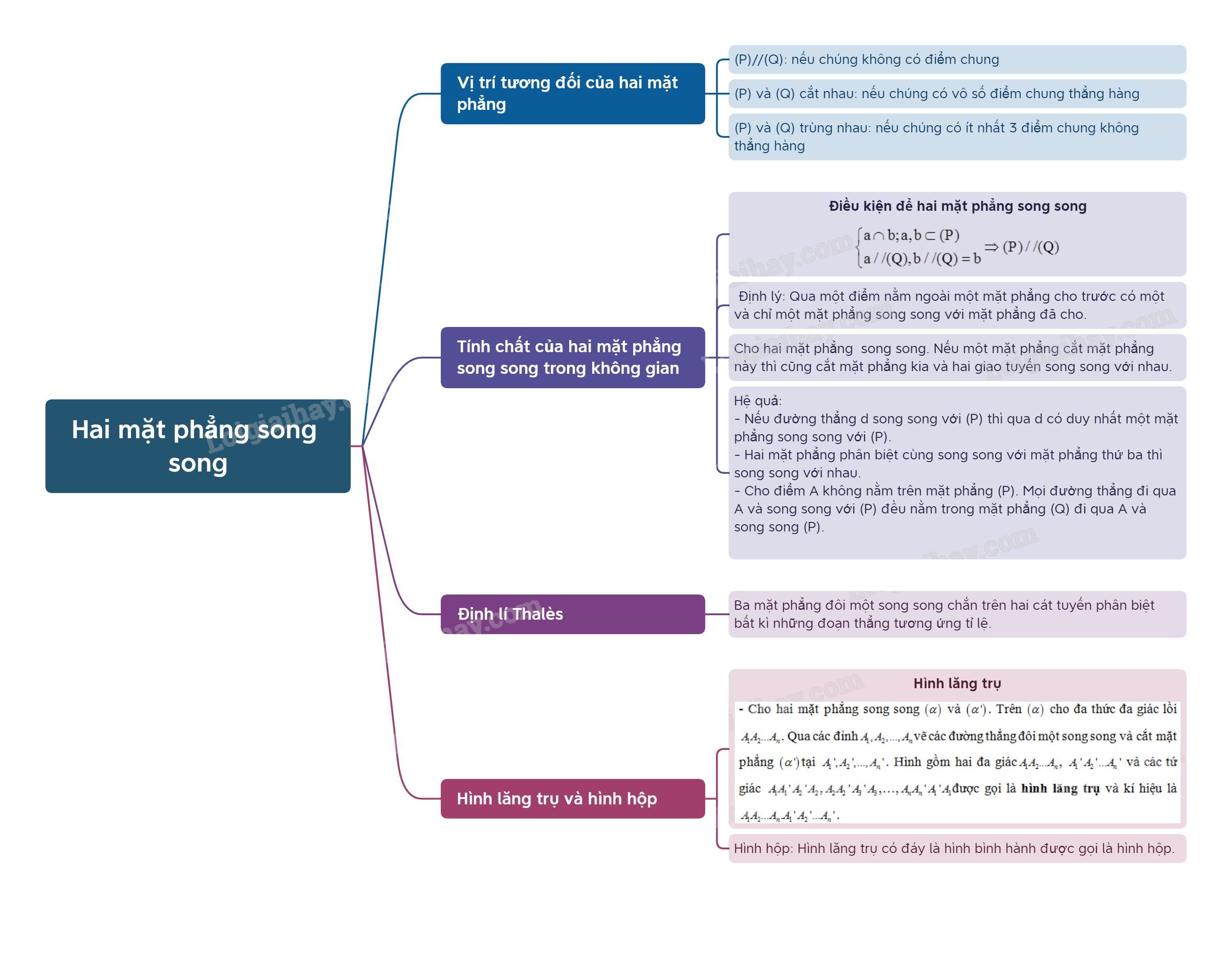
Lý thuyết Hai mặt phẳng song song - Toán 11
Chào mừng bạn đến với bài học về Lý thuyết Hai mặt phẳng song song trong chương trình SGK Toán 11.
Đây là một phần kiến thức quan trọng trong chương Hình học không gian, giúp bạn hiểu rõ hơn về mối quan hệ giữa các mặt phẳng trong không gian ba chiều.
Chúng ta sẽ cùng nhau khám phá định nghĩa, điều kiện nhận biết, và các tính chất quan trọng của hai mặt phẳng song song.
I. Hai mặt phẳng song song trong không gian
I. Hai mặt phẳng song song trong không gian
* Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm chung.

*Lưu ý: \(\left\{ \begin{array}{l}\left( \alpha \right)//\left( \beta \right)\\d \subset \left( \alpha \right)\end{array} \right. \Rightarrow d//\left( \beta \right)\).
II. Tính chất của hai mặt phẳng song song trong không gian
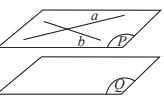
- Điều kiện để hai mặt phẳng song song: Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng cắt nhau a,b và a,b cùng song song với mặt phẳng phẳng \(\left( Q \right)\)thì \(\left( P \right)\)song song với \(\left( Q \right)\)
- Định lí 2: Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
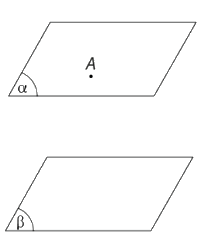
* Hệ quả:
- Nếu đường thẳng d song song với \(\left( \alpha \right)\) thì qua d có duy nhất một mặt phẳng song song với \(\left( \alpha \right)\)
- Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
- Cho điểm A không nằm trên mặt phẳng \(\left( \alpha \right)\) .Mọi đường thẳng đi qua A và song song với \(\left( \alpha \right)\)đều nằm trong mặt phẳng đi qua A và song song \(\left( \alpha \right)\).
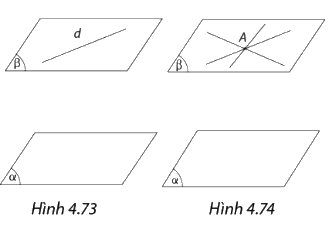
- Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
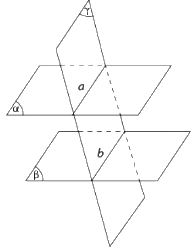
III. Định lí Thalès
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.
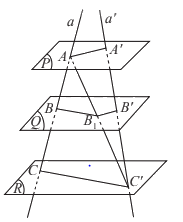
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\)
IV. Hình lăng trụ và hình hộp
- Cho hai mặt phẳng song song \(\left( \alpha \right)\) và \(\left( {\alpha '} \right)\). Trên \(\left( \alpha \right)\) cho đa thức đa giác lồi \({A_1}{A_2}...{A_n}\). Qua các đỉnhvẽ các đường thẳng đôi một song song và cắt mặt phẳng \(\left( {\alpha '} \right)\)tại \({A_1}',{A_2}',...,{A_n}'\). Hình gồm hai đa giác\({A_1}{A_2}...{A_n}\), \({A_1}'{A_2}'...{A_n}'\) và các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\)được gọi là hình lăng trụ và kí hiệu là \({A_1}{A_2}...{A_n}.{A_1}'{A_2}'...{A_n}'\).
- Các điểm \({A_1},{A_2},...,{A_n}\) và \({A_1}',{A_2}',...,{A_n}'\)được gọi là các đỉnh, các đoạn thẳng \({A_1}{A_1}',{A_2}{A_2}',...,{A_n}{A_n}'\)được gọi là các cạnh bên, các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_n}{A_1}\)và \({A_1}'{A_2}',{A_2}'{A_3}',...,{A_n}'{A_1}'\) gọi là cạnh đáy của hình trụ.
- Hai đa giác \({A_1}{A_2}...{A_n}\)và \({A_1}'{A_2}'...{A_n}'\)được gọi là hai mặt đáy của hình lăng trụ.
Các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\) gọi là các mặt bên của hình trụ.
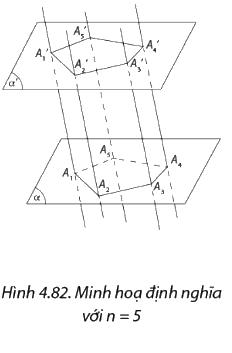
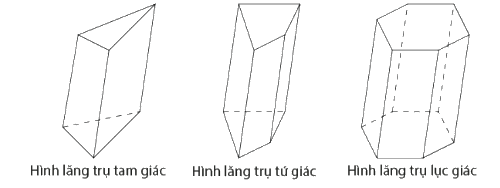
- Hình lăng trụ có đáy là tam giác, tứ giác, ngũ giác,…tương ứng được gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác,…
2.Hình hộp
Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.
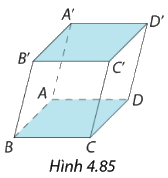
- Trong hình hình hộp có:
+ Sáu mặt là sau hình bình hành. Mỗi mặt đều có một mặt song song với nó gọi là haimặt đối diện.
+ Hai đỉnh không cùng nằm trưn một mặt gọi là hai đỉnh đối diện.
+ Đoạn thẳng nối 2 đỉnh đối diện gọi là đường chéo.
+ Bốn đường chéo cắt nhau tại trung điểm mỗi đường.
Lý Thuyết Hai Mặt Phẳng Song Song - SGK Toán 11 Cùng Khám Phá
Trong chương trình Hình học không gian lớp 11, kiến thức về hai mặt phẳng song song đóng vai trò then chốt. Việc nắm vững lý thuyết này không chỉ giúp bạn giải quyết các bài tập trong SGK mà còn là nền tảng cho các kiến thức nâng cao hơn.
1. Định Nghĩa Hai Mặt Phẳng Song Song
Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung. Điều này có nghĩa là, nếu bạn cố gắng tìm một điểm nào đó thuộc cả hai mặt phẳng, bạn sẽ không tìm thấy.
2. Điều Kiện Nhận Biết Hai Mặt Phẳng Song Song
Có một số điều kiện để nhận biết hai mặt phẳng song song:
- Điều kiện 1: Nếu hai mặt phẳng có hai đường thẳng song song nằm trong mỗi mặt phẳng thì hai mặt phẳng đó song song.
- Điều kiện 2: Nếu một mặt phẳng chứa một đường thẳng song song với một mặt phẳng khác và mặt phẳng đó không chứa đường thẳng đó thì hai mặt phẳng song song.
- Điều kiện 3: Nếu hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì hai mặt phẳng đó song song với nhau.
3. Tính Chất của Hai Mặt Phẳng Song Song
Hai mặt phẳng song song có những tính chất quan trọng sau:
- Qua một điểm nằm ngoài mặt phẳng, có duy nhất một mặt phẳng song song với mặt phẳng đã cho.
- Nếu một mặt phẳng cắt một trong hai mặt phẳng song song thì nó cũng cắt mặt phẳng còn lại.
4. Ứng Dụng của Lý Thuyết Hai Mặt Phẳng Song Song
Lý thuyết này được ứng dụng rộng rãi trong việc giải các bài toán về hình học không gian, đặc biệt là:
- Xác định mối quan hệ giữa các mặt phẳng.
- Chứng minh các tính chất liên quan đến hình chóp, hình lăng trụ.
- Tính góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng.
5. Bài Tập Vận Dụng
Để hiểu rõ hơn về lý thuyết này, chúng ta hãy xem xét một số bài tập vận dụng:
Bài tập 1: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng mặt phẳng (SAM) song song với mặt phẳng (BCD).
Bài tập 2: Cho hai mặt phẳng (P) và (Q) song song với nhau. Trên (P) có điểm A và trên (Q) có điểm B. Tìm tập hợp các điểm M sao cho góc AMB bằng 90 độ.
6. Mở Rộng và Liên Hệ
Lý thuyết hai mặt phẳng song song là cơ sở để hiểu các khái niệm phức tạp hơn trong hình học không gian như:
- Góc giữa hai mặt phẳng.
- Khoảng cách giữa hai mặt phẳng song song.
- Các bài toán về thiết diện của hình chóp và hình lăng trụ.
7. Lời Khuyên Khi Học Lý Thuyết
Để học tốt lý thuyết hai mặt phẳng song song, bạn nên:
- Nắm vững định nghĩa và các điều kiện nhận biết.
- Hiểu rõ các tính chất của hai mặt phẳng song song.
- Luyện tập thường xuyên các bài tập vận dụng.
- Vẽ hình minh họa để hình dung rõ hơn về các khái niệm.
Hy vọng với những kiến thức trên, bạn đã có cái nhìn tổng quan và hiểu rõ hơn về Lý thuyết Hai mặt phẳng song song - SGK Toán 11. Chúc bạn học tập tốt!