Lý Thuyết Góc Lượng Giác - SGK Toán 11

Lý thuyết Góc lượng giác - SGK Toán 11 Cùng khám phá

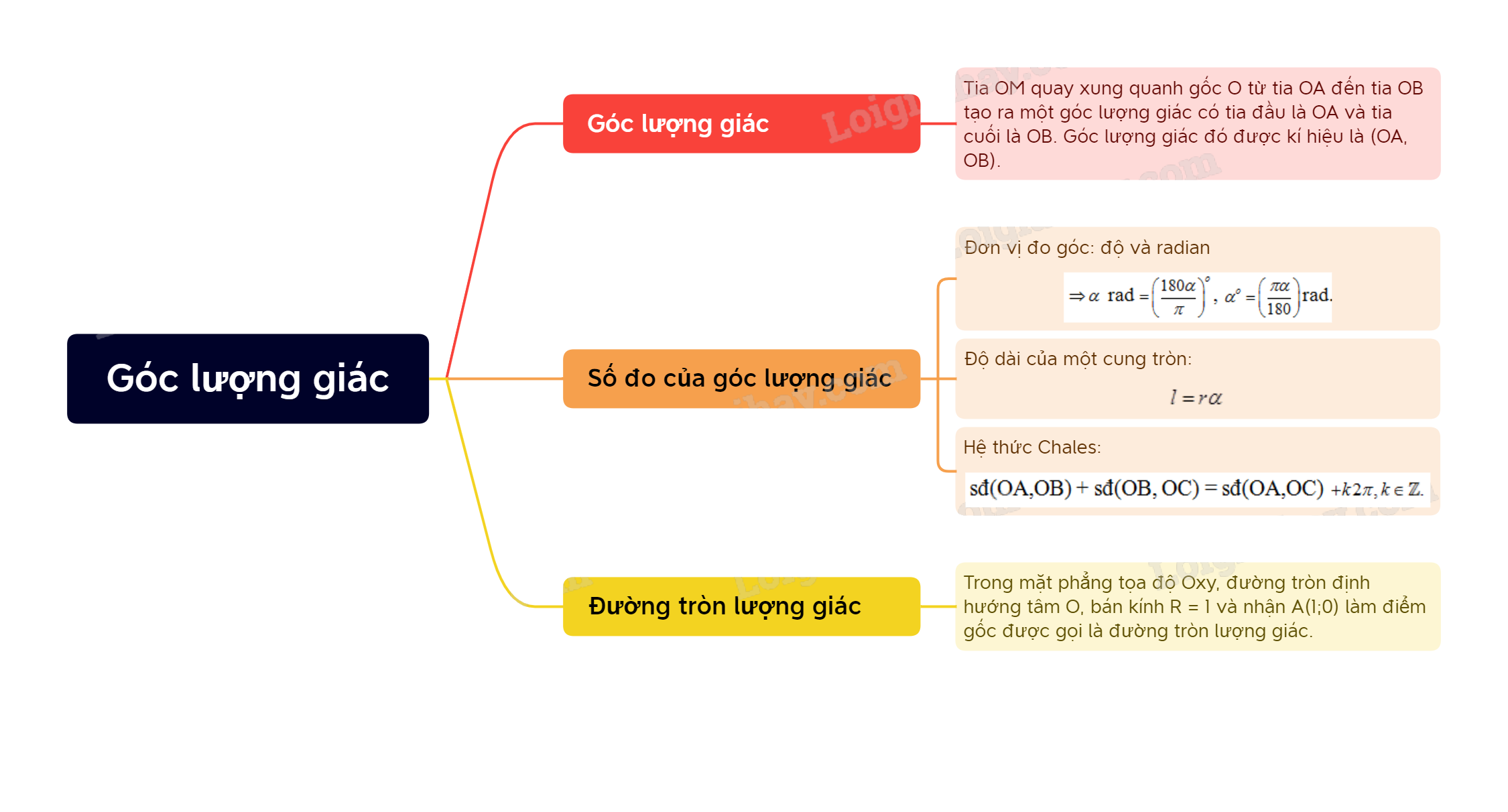
Lý thuyết Góc lượng giác - SGK Toán 11

Góc lượng giác là một trong những kiến thức nền tảng và quan trọng của chương trình Toán 11. Việc nắm vững lý thuyết này không chỉ giúp bạn giải quyết các bài tập trong SGK mà còn là bước đệm vững chắc cho các kiến thức nâng cao hơn trong chương trình học.

Tại tusach.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, chi tiết và dễ hiểu về Lý thuyết Góc lượng giác - SGK Toán 11, giúp bạn học tập hiệu quả và đạt kết quả tốt nhất.

I. Khái niệm góc lượng giác

I. Khái niệm góc lượng giác

Đường tròn định hướng

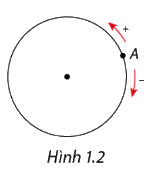
Lý thuyết Góc lượng giác - SGK Toán 11 Cùng khám phá 1

Ta quy ước chiều ngược với chiều quay của kim đồng hồ là chiều dương.

Góc lượng giác

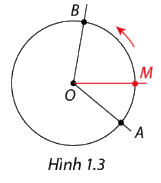
Lý thuyết Góc lượng giác - SGK Toán 11 Cùng khám phá 2

- Tia OM quay xung quanh gốc O từ tia OA đến tia OB tạo ra một góc lượng giác có tia đầu là OA và tia cuối là OB. Góc lượng giác đó được kí hiệu là (OA,OB).

- Điểm M cũng tạo ra một cung lượng giác có điểm đầu A và điểm cuối B. Cung lượng giác đó được kí hiệu là .

*Lưu ý: Có vô số góc lượng giác tia đầu OA, tia cuối OB và cũng có vô số cung lượng giác có điểm đầu A và điểm cuối B.

II. Số đo của góc lượng giác

1. Độ và radian

a, Đơn vị radian

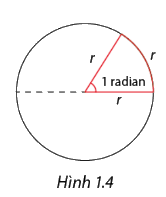
Lý thuyết Góc lượng giác - SGK Toán 11 Cùng khám phá 3

- Trên đường tròn tùy ý, cung có độ dài bằng bán kính được gọi là cung có số do 1 radian.

- Góc ở tâm chắn cung có số đo 1 radian được gọi là góc có số đo 1 radian.

- Radian được viết tắt là rad.

b, Quan hệ giữa độ và radian

Ta có: 1 rad \( = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \left( {\frac{\pi }{{180}}} \right)\)rad.

\( \Rightarrow \alpha \) rad \( = {\left( {\frac{{180\alpha }}{\pi }} \right)^o}\), \({\alpha ^o} = \left( {\frac{{\pi \alpha }}{{180}}} \right)\)rad.

c, Độ dài của một cung tròn

Lý thuyết Góc lượng giác - SGK Toán 11 Cùng khám phá 4

Một cung tròn của đường tròn bán kính r và có số đo \(\alpha \)rad thì có độ dài \(l = r\alpha \).

2. Số đo của góc lượng giác

Số đo của góc lượng giác (OA,OB), kí hiệu là sđ(OA,OB), là số đo của cung lượng giác tương ứng.

* Hệ thức Chasles

Với 3 tia OA, OB, OC bất kì ta có:

sđ(OA,OB) + sđ(OB, OC) = sđ(OA,OC) \( + k2\pi ,k \in \mathbb{Z}.\)

3. Đường tròn lượng giác

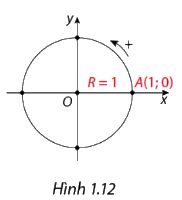
Lý thuyết Góc lượng giác - SGK Toán 11 Cùng khám phá 5

Trong mặt phẳng tọa độ Oxy, đường tròn định hướng tâm O, bán kính R = 1 và nhận A(1;0) làm điểm gốc được gọi là đường tròn lượng giác.

Lý thuyết Góc lượng giác - SGK Toán 11 Cùng khám phá 6

Lý Thuyết Góc Lượng Giác - SGK Toán 11: Tổng Quan và Hướng Dẫn Chi Tiết

Chào mừng các em học sinh đến với chuyên mục lý thuyết Góc lượng giác của môn Toán 11. Đây là một phần kiến thức quan trọng, nền tảng cho nhiều chương sau. Bài viết này sẽ cung cấp một cái nhìn tổng quan, chi tiết và dễ hiểu về các khái niệm, định nghĩa, công thức và ứng dụng của góc lượng giác, dựa trên nội dung SGK Toán 11.

1. Định Nghĩa Góc Lượng Giác

Trong hình học, chúng ta đã quen với khái niệm góc trong khoảng từ 0° đến 180°. Tuy nhiên, trong lượng giác, khái niệm góc được mở rộng hơn rất nhiều. Góc lượng giác là một góc được tạo bởi việc quay một tia từ vị trí ban đầu (tia Ox) đến vị trí cuối (tia Ot). Chiều quay có thể là chiều dương (ngược chiều kim đồng hồ) hoặc chiều âm (cùng chiều kim đồng hồ).

Độ (°): Đơn vị đo góc truyền thống. Một vòng tròn đầy đủ là 360°.
Radian (rad): Đơn vị đo góc trong hệ đo lường quốc tế. Một radian là góc tạo bởi hai bán kính của một đường tròn, chắn một cung có độ dài bằng bán kính của đường tròn đó.
Công thức chuyển đổi: 180° = π rad

2. Các Hàm Số Lượng Giác của Góc Lượng Giác

Các hàm số lượng giác (sin, cos, tan, cot) là những công cụ quan trọng để mô tả mối quan hệ giữa các cạnh của một tam giác vuông và các góc của nó. Trong trường hợp góc lượng giác, chúng ta mở rộng định nghĩa này cho mọi góc.

Hàm số	Ký hiệu	Định nghĩa
Sin	sin(α)	Tỷ số giữa cạnh đối và cạnh huyền
Cos	cos(α)	Tỷ số giữa cạnh kề và cạnh huyền
Tan	tan(α)	Tỷ số giữa cạnh đối và cạnh kề
Cot	cot(α)	Tỷ số giữa cạnh kề và cạnh đối

3. Các Công Thức Lượng Giác Cơ Bản

Việc nắm vững các công thức lượng giác là rất quan trọng để giải các bài toán liên quan đến góc lượng giác. Dưới đây là một số công thức cơ bản:

sin²(α) + cos²(α) = 1
tan(α) = sin(α) / cos(α)
cot(α) = cos(α) / sin(α)
1 + tan²(α) = 1/cos²(α)
1 + cot²(α) = 1/sin²(α)

4. Giá Trị Lượng Giác của Các Góc Đặc Biệt

Các góc đặc biệt như 0°, 30°, 45°, 60°, 90° có giá trị lượng giác quen thuộc. Việc ghi nhớ các giá trị này sẽ giúp bạn giải quyết bài tập nhanh chóng và chính xác hơn.

Ví dụ:

sin(0°) = 0
cos(0°) = 1
sin(30°) = 1/2
cos(30°) = √3/2

5. Ứng Dụng của Góc Lượng Giác

Góc lượng giác có rất nhiều ứng dụng trong thực tế, bao gồm:

Đo đạc khoảng cách và chiều cao: Sử dụng các hàm số lượng giác để tính toán khoảng cách và chiều cao của các vật thể.
Điều hướng và định vị: Trong hàng hải, hàng không và các lĩnh vực liên quan đến định vị, góc lượng giác được sử dụng để xác định vị trí và hướng đi.
Vật lý: Góc lượng giác được sử dụng để mô tả các hiện tượng vật lý như dao động, sóng và chuyển động tròn.

Hy vọng bài viết này đã cung cấp cho các em một cái nhìn tổng quan và chi tiết về Lý thuyết Góc lượng giác - SGK Toán 11. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài tập. Chúc các em học tập tốt!